Cho hai tập hợp A = { x ∈ ℝ : − 7 ≤ x ≤ 3 } , B = { x ∈ ℝ : − 1 < x < 5 } .
Tập hợp A ∩ B là:
A. ( − 1 ; 3 )
B. [ − 1 ; 3 )
C. ( − 1 ; 3 ]
D. ( 3 ; 5 )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 7 2017
Ta có B = x ∈ R : − 3 < x ≤ 5 = − 3 ; 5
khi đó A ∩ B = − 3 ; 1
Đáp án A
CM
11 tháng 11 2018
Đáp án C.
Giải thích
M = x ∈ R : x ≥ - 3 = [ - 3 ; + ∞ ) N = x ∈ R : - 2 ≤ x ≤ 1 = [ - 2 ; 1 ] P = x ∈ R : - 5 < x ≤ 0 = ( - 5 ; 0 ]
Ta thấy rằng - 2 ; 1 ⊂ [ - 3 ; + ∞ ) d o đ ó N ⊂ M
CM
23 tháng 6 2019
Đáp án: B
( x2 + 1)(x - 2) > 0 ⇔ x - 2 > 0 (do x2 + 1 > 0 ∀x ∈ R)
⇔ x > 2 => B = (2; ∞ ).
Để A ∪ B = R thì m ≥ 2
CM
16 tháng 5 2019
Đáp án: C
1 x - 5 > 1 3 ⇔ x - 5 < 3 ⇔ - 3 < x - 5 < 3 ⇔ 2 < x < 8 ⇒ N = ( 2 ; 8 ) . M \ N = ( - 2 ; 2 ] ; C ℝ P = ℝ \ P = ( - ∞ ; 1 ) ( M \ N ) ∪ C ℝ P = ( - ∞ ; 2 ] .
CM
1 tháng 3 2019
Đáp án: A
1 x - 2 > 1 ⇔ x - 2 < 1 ⇔ - 1 < x - 2 < 1 ⇔ 1 < x < 3 ⇒ Q = ( 1 ; 3 ) ( P ∩ Q ) = ( 1 ; 3 ) ; ( P ∪ Q ) = [ - 1 ; + ∞ ) ( P ∪ Q ) \ ( P ∩ Q ) = [ - 1 , 1 ] ∪ [ 3 ; + ∞ ) .
CM
25 tháng 5 2019
Đáp án B
Ta có:
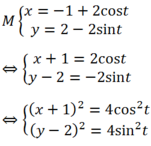
=> ( x +1) 2+ (y- 2) 2= 4cos2t + 4sin2t
=> ( x +1) 2+ (y- 2) 2 = 4
Vậy tập hợp điểm M là phương trình đường tròn có tâm I( -1;2) , bán kính R= 2.
CM
5 tháng 11 2018
A = x ∈ ℝ : | x | ≥ 2 = − ∞ ; − 2 ∪ 2 ; + ∞ ⇒ C ℝ A = ℝ \ A = ( − 2 ; 2 )
Đáp án B
Đáp án C