Tập nghiệm của bất phương trình |2x - 1| > x + 2 là:
A. - 2 ; - 1 3 ∪ [ 3 ; + ∞ )
B. - ∞ ; - 1 3 ∪ [ 3 ; + ∞ )
C. ( - ∞ ; - 2 ]
D. [ 3 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Ta có :
2 x + 2 > 3 ( 2 - x ) + 1 ⇔ 2 x + 2 > 6 - 3 x + 1 ⇔ 5 x > 5 ⇔ x > 1 .
Vậy tập nghiệm của bất phương trình 2 x + 2 > 3 ( 2 - x ) + 1 là 1 ; + ∞ .
Đáp án là A.

Tập nghiệm của BPT là: \(\left[{}\begin{matrix}-3< x\le-1\\0\le x< 1\\x>1\end{matrix}\right.\)

Chọn D.
Điều kiện: x ≠ -2;1
Khi đó, ta có:
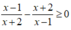
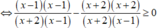
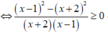
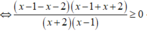
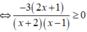
Lập bảng xét dấu.
Tập nghiệm của bất phương trình 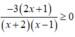 là
là 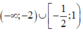 .
.

Chọn B.
Ta có:
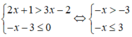
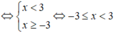
Tập nghiệm của hệ bất phương trình là S = [-3;3).
Đáp án B.
Ta có:
|2x - 1| ≥ x + 2 ⇔ x + 2 < 0
hoặc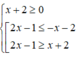
• x + 2 < 0 ⇔ x < -2 (1)
•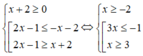
Kết hợp (1) và (2) ta có nghiệm của bất phương trình là: