Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
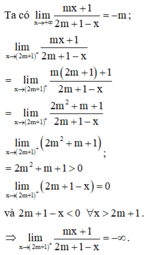
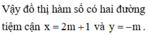
Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 3 suy ra
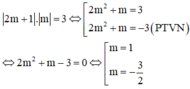
Đáp án: D.
Tiệm cận đứng của đồ thị hàm số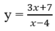 
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.
Đáp án A
Đồ thị hàm số có đường tiệm cận ngang là y = 2 3 và tiệm cận đứng là x = − 1 3 .
Do đó diện tích hình chữ nhật cần tính là:
S
=
2
3
.
−
1
3
=
2
9
.
Đáp án A
Vì I là tâm đối xứng của đồ thị C ⇒ I 2 ; 2
Gọi M x 0 ; 2 x 0 − 1 x 0 − 2 ∈ C ⇒ y ' x 0 = − 3 x 0 − 2 2 suy ra phương trình tiếp tuyến Δ là
y − y 0 = y ' x 0 x − x 0 ⇔ y − 2 x 0 − 1 x 0 − 2 = − 3 x 0 − 2 2 x − x 0 ⇔ y = − 3 x 0 − 2 2 + 2 x 0 2 − 2 x 0 + 2 x 0 − 2 2
Đường thẳng Δ cắt TCĐ tại A 2 ; y A → y A = 2 x 0 + 2 x 0 − 2 ⇒ A 2 ; 2 x 0 + 2 x 0 − 2
Đường thẳng Δ cắt TCN tại B x B ; 2 → x B = 2 x 0 − 2 ⇒ B 2 x 0 − 2 ; 2
Suy ra I A = 6 x 0 − 2 ; I B = 2 x 0 − 2 → I A . I B = 6 x 0 − 2 .2 x 0 − 2 = 12
Tam giác IAB vuông tại I ⇒ R Δ I A B = A B 2 = I A 2 + I B 2 2 ≥ 2 I A . I B 2 = 6
Dấu bằng xảy ra khi và chỉ khi I A = I B ⇔ 3 = x 0 − 2 2 ⇔ x 0 = 2 + 3 x 0 = 2 − 3
Suy ra phương trình đường thẳng Δ và gọi M, N lần lượt là giao điểm của Δ với Ox, Oy
Khi đó M 2 x 0 2 − 2 x 0 + 2 3 ; 0 , N 0 ; 2 x 0 2 − 2 x 0 + 2 3 ⇒ S Δ O M N = 1 2 O M . O N
Vậy S m a x = 14 + 8 3 ≈ 27 , 85 ∈ 27 ; 28 k h i x 0 = 2 + 3
Đáp án: D.
Tiệm cận đứng của đồ thị hàm số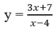 
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.
