Số nào sau đây là số thực?
A. 2 + i 2 1 - i 2 + 1 + i 2 2 - i 2
B. (2 + 3i)(3 - i) + (2 - 3i)(3 + i)
C. 1 + i 2 - i 2 - i + 1 + i 2 - i 2 + i
D. 2 + i 3 2 - 2 - i 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng (1+i)2 = 1+2i+i2 = 1+2i – 1 = 2i
Cách giải:
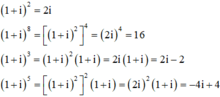
Như vậy, chỉ có số phức (1+i)8 là số thực

Đáp án B
Phương pháp:
Sử dụng ![]()
Cách giải:
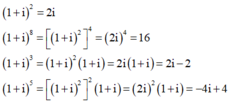
Như vậy, chỉ có số phức ![]() là số thực
là số thực

Đáp án B
|
|
Số lượng NST của từng cặp |
Dạng đột biến |
|||
| Thể đột biến |
I |
II |
III |
IV |
|
| A |
4 |
4 |
4 |
4 |
4n |
| B |
3 |
3 |
3 |
3 |
3n |
| C |
2 |
4 |
2 |
2 |
2n+2 |
| D |
1 |
2 |
2 |
2 |
2n-1 |
2n = 8 → Có 4 cặp NST, mỗi cặp có 2 NST
Thể đột biến A: 4 cặp mỗi cặp đều có 4 NST → 4n → A có thể được hình thành qua nguyên phân khi conxixin tác động gây đột biến đa bội 2n→ 4n; hoặc qua giảm phân khi tất cả các cặp NST rối loạn giảm phân 2 → B đúng
Thể đột biến B: mỗi cặp có 3 chiếc NST → tam bội 3n = 12 hình thành giao tử chiếm n NST với xác suất 1/3 và được hình thành qua thụ tinh giữa 2n và 4n→ A và C sai
Thể đột biến C có cặp NST số 2 có 4 chiếc, xảy ra đột biến lệch bội 2n+2 hình thành qua nguyên phân → D sai
Thể đột biến D có cặp NST số 1 có 1 chiếc, xảy ra đột biến lệch bội 2n – 1 hình thành qua nguyên phân → D sai
Đáp án B