Cho tứ diện đểu ABCD cạnh A. Gọi O là tâm của tam giác đểu BCD. M, N lần lượt là trung điểm của AC, AB. Quay hình thang BCMN quanh đường thẳng AO ta được khối tròn xoay có thể tích là bao nhiêu?
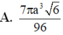
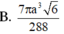
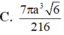
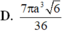
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
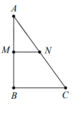
Xét khối nón tròn xoay ( N 1 ) được tạo thành khi quay tam giác AMN quanh trục A B ⇒ N 1 có bán kính đáy r 1 = M N = 2 ; chiều cao h 1 = A M = 5 . Suy ra thể tích khối nón ( N 1 ) là V 1 = 1 3 πr 1 2 h = 1 3 π . 2 2 . 5 = 20 π 3 .
Xét khối nón tròn xoay N 2 được tạo thành khi quay tam giác ABC
quanh trục A B ⇒ N 2 có bán kính đáy r 2 = B C = 4 ; chiều cao h 2 = A B = 10 .
Suy ra thể tích khối nón N 2 là V 2 = 1 3 πr 2 2 h 2 = 1 3 π . 4 2 . 10 = 160 π 3 .
Vậy thể tích khối tròn xoay cần tính là V = V 1 - V 2 = 160 π 3 - 20 π 3 = 140 π 3 .
Đáp án B
Gọi các điểm như hình vẽ
Gọi V là thể tích khối tròn xoay khi xoay hình thang BCMN quanh đường thẳng AO
Ta có: tam giác IMN và tam giác OBC là hai tam giác cân tại I, O và lần lượt nằm trong 2 mặt phẳng vuông góc với trục AO nên khi xoay hình thang BCMN quanh đường thẳng AO ta được khối tròn xoay bị giới hạn bởi hai hình nón cụt được tạo ra khi quay tứ giác IMBO quanh trục AO và hình nón cụt được tạo ra khi quay tứ giác IKHO quanh trục AO
Lại có: