Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng R. Tính thể tích V của khối trụ
(
T
)
. ...
Đọc tiếp
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng R. Tính thể tích V của khối trụ ( T ) .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
CM
19 tháng 6 2017
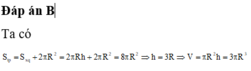
Đáp án B
Ta có S t p = S x q + 2 πR 2 = 2 πRh + 2 πR 2 = 8 πR 2 ⇒ h = 3 R ⇒ V = πR 2 h = 3 πR 3
CM
10 tháng 1 2017
Đáp án B.
Diện tích toàn phần hình trụ (T) là 
⇔ h = 3R
Thể tích của khối trụ (T) là
CM
11 tháng 9 2019
Chọn B.
Phương pháp:
Thiết diện qua trục của hình trụ có bán kính đáy R và chiều cao h là hình chữ nhật có kích thước 2R × h. Thể tích khối trụ bán kính đáy R và chiều cao h là V = πR 2 h .
Cách giải:
Một mặt phẳng qua trục cắt khối trụ theo thiết diện là một hình chữ nhật có diện tích bằng 16a2
⇒ 2 R . 2 R = 16 a 2 ⇔ R 2 = 4 a 2 ⇔ R = 2 a ⇒ h = 2 R = 4 a
Thể tích của khối trụ đã cho: V = πR 2 h = π . ( 2 a ) 2 . 4 a = 16 πa 3 .
CM
18 tháng 9 2018
Đáp án D
Ta có V t = V = l . π R 2 ⇒ l = V π R 2
S t = l .2 π R + 2 π R 2 ⇒ S t = V π R 2 π R + 2 π R 2 = 2 ( π R 2 + V R )
S t = 2 ( π R 2 + V 2 R + V 2 R ) ≥ 2.3 π R 2 . V 2 R . V 2 R 3 = 6 π V 2 4 3
Dấu “=” xảy ra khi và chỉ khi π R 2 = V 2 R ⇔ R = V 2 π 3