Chứng minh các đẳng thức sau:
a) − u 2 + 3 u − 2 ( u + 2 ) ( u − 1 ) = u 2 − 4 u + 4 4 − u 2 với u ≠ ± 2 và u ≠ 1 ;
b) v 3 + 27 v 2 − 3 v + 9 = v + 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

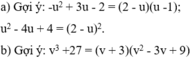

a: \(\dfrac{x^2-3x+2}{x^2-1}=\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-2}{x+1}\)
\(a,VP=\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-2}{x+1}=VP\\ b,VT=\dfrac{u\left(4u^2-1\right)}{5\left(1-2u\right)}=\dfrac{-u\left(1-2u\right)\left(1+2u\right)}{5\left(1-2u\right)}=\dfrac{-u\left(1+2u\right)}{5}=-\dfrac{2u^2+u}{5}=VP\)


a)\(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
\(\Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\)
\(\Leftrightarrow0\le2a^2-a^2+2b^2-b^2-2ab\)
\(\Leftrightarrow0\le a^2-2ab+b^2\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
=> Đúng
b) \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3a^2+3b^2+3c^2\)
\(\Leftrightarrow0\le3a^2-a^2+3b^2-b^2+3c^2-c^2-2ab-2bc-2ac\)
\(\Leftrightarrow0\le2a^2+2b^2+2c^2-2ab-2bc-2ac\)
\(\Leftrightarrow0\le\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
=> Đúng
a,Ta có : \(\left(a+b\right)^2+\left(a-b\right)^2=2\left(a^2+b^2\right)\)
Do : \(\left(a-b\right)^2\ge0\)nên \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\).
b, Xét : \(\left(a+b+c\right)^2+\left(a-b\right)^2-\left(a-c\right)^2+\left(b-c\right)^2\) . Khai triển và rút gọn, ta được :
\(3\left(a^2+b^2+c^2\right)\) . Vậy : \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)

1/
a, \(4x^2+36xy+81y^2=\left(2x+9y\right)^2\)
b, \(12y+\frac{9}{100}y^2+400=\left(\frac{3}{10}y+20\right)^2\)
2/
\(2bc+b^2+c^2-a^2=\left(b+c\right)^2-a^2=\left(a+b+c\right)\left(b+c-a\right)=2p\left(b+c-a\right)\) (1)
Ta có: a+b+c=2p => b+c=2p-a (2)
Thay (2) và (1) ta có:
\(2p\left(2p-a-a\right)=2p\left(2p-2a\right)=4p\left(p-a\right)\) (đpcm)
3/
Gọi 2 số tự nhiên chẵn là 2k và 2k+2 (k thuộc N)
Theo bài ra ta có: \(\left(2k+2\right)^2-\left(2k\right)^2=36\)
=> \(\left(2k+2-2k\right)\left(2k+2+2k\right)=36\)
=>\(2\left(4k+2\right)=36\)
=>\(8k+4=36\)
=>\(8k=32\)
=> k = 4
=> \(2k=8;2k+2=10\)
Vậy...

\(\left|x\left(u+v\right)-y\left(u-v\right)\right|^2\le\left(x^2+y^2\right)\left[\left(u+v\right)^2+\left(u-v\right)^2\right]=1\cdot\left(2u^2+2v^2\right)=2\)
\(\Rightarrow\left|x\left(u+v\right)-y\left(u-v\right)\right|\le\sqrt{2}\)
@Hải Ngọc Cảm ơn câu trả lời của bạn, nhưng ở đoạn đầu bạn nhầm dấu cộng thành dấu trừ rồi! :))

\(VP=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}+\sqrt{\frac{a-\sqrt{a^2-b}}{2}}\)
\(VP^2=\frac{a+\sqrt{a^2-b}}{2}+\frac{a-\sqrt{a^2-b}}{2}+2\sqrt{\frac{\left(a+\sqrt{a^2-b}\right)\left(a-\sqrt{a^2-b}\right)}{2.2}}\)
\(=a+\sqrt{\left[a^2-\left(a^2-b\right)\right]}=a+\sqrt{b}\)
\(\Rightarrow VP=\sqrt{a+\sqrt{b}}=VT\)

Câu 4:
a) C/m tương đương
\(\dfrac{a+b}{2}\ge\sqrt{ab}\) \(\Leftrightarrow a+b-2\sqrt{ab}\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)\ge0\) => luôn đúng
=> \(\dfrac{a+b}{2}\ge\sqrt{ab}\Rightarrowđpcm\)
b) \(\dfrac{bc}{a}+\dfrac{ca}{b}+\dfrac{ab}{c}\ge a+b+c\)
Áp dụng BĐT: \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\)
+) \(\dfrac{bc}{a}+\dfrac{ba}{c}=b\left(\dfrac{c}{a}+\dfrac{a}{c}\right)\ge2b\)
+) \(\dfrac{ca}{b}+\dfrac{cb}{a}=c\left(\dfrac{a}{b}+\dfrac{b}{a}\right)\ge2c\)
+) \(\dfrac{ab}{c}+\dfrac{ac}{b}=a\left(\dfrac{b}{c}+\dfrac{c}{b}\right)\ge2a\)
Cộng vế vs vế ta có:
\(2\left(\dfrac{bc}{a}+\dfrac{ca}{b}+\dfrac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(\Leftrightarrow\dfrac{bc}{a}+\dfrac{ca}{b}+\dfrac{ab}{c}\ge a+b+c\Rightarrowđpcm\)
c) Áp dụng BĐT Cô-si cho 2 số không âm ta có:
\(12^2=\left(3a+5b\right)^2\ge4.3a.5b=60ab\)
=> \(ab\le\dfrac{12}{5}\)
Vậy GTLN của P là \(\dfrac{12}{5}\)
Dấu ''=" xảy ra khi \(3a=5b\), từ đó ta có hệ
\(\left\{{}\begin{matrix}3a=5b\\3a+5b=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{6}{5}\end{matrix}\right.\)