Trừ các phân thức sau:
a) x + 1 x − 5 − 1 − x x + 5 − 2 x ( 1 − x ) 25 − x 2 với x ≠ ± 5 ;
b) m 2 + 1 − m 4 − 4 m 2 + 3 m 2 − 1 với m ≠ ± 1 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

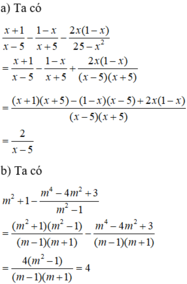

a: \(=\dfrac{3b+4a}{6ab}\)
b: \(=\dfrac{x^2-2x+1-x^2-2x-1}{x^2-1}=\dfrac{-4x}{x^2-1}\)
c: \(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xy}{xyz}=\dfrac{z-x}{xz}\)
d: \(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: \(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)

`a, a/(a-3) - 3/(a+3) = (a(a+3) - 3(a-3))/(a^2-9)`
`= (a^2+9)/(a^2-9)`
`b, 1/(2x) + 2/x^2 = x/(2x^2) + 4/(2x^2) = (x+4)/(2x^2)`
`c, 4/(x^2-1) - 2/(x^2+x) = (4x)/(x(x-1)(x+1)) - (2(x-1))/(x(x+1)(x-1))`
`= (2x+2)/(x(x-1)(x+1)`
`= 2/(x(x-1))`

\(a,=\dfrac{4y.5x^3}{3x^2.2y^3}=\dfrac{20x^3y}{6x^2y^3}=\dfrac{10x}{3y^2}\\ b,=\dfrac{\left(x-1\right)^2.x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2.x.\left(x+1\right)}{\left(x-1\right)^2.\left(x+1\right)}=x\)
\(c,=\dfrac{x\left(2+x\right).3\left(x^3+1\right)}{\left(x^2-x+1\right).3.\left(x+2\right)}=\dfrac{3x.\left(x+2\right).\left(x+1\right)\left(x^2-x+1\right)}{\left(x^2-x+1\right).3\left(x+2\right)}=x\left(x+1\right)\)


a) \(P\left(x\right)-x\left(x+5\right)-\left(2x-3\right)+x^2\left(3x-2\right)\)
\(P\left(x\right)=-x^2-5x-2x+3+3x^3-2x^2\)
\(P\left(x\right)=3x^3+\left(-x^2-2x^2\right)-\left(5x+2x\right)+3\)
\(P\left(x\right)=3x^3-3x^2-7x+3\)
b) \(Q\left(x\right)=2x\left(x+1\right)+3x\left(5-x\right)-7\left(x-5\right)\)
\(Q\left(x\right)=2x^2+2x+15x-3x^2-7x+35\)
\(Q\left(x\right)=-x^2+10x+35\)
a: P(x)=-x^2-5x-2x+3+3x^3-2x^2
=3x^3-3x^2-7x+3
b: Q(x)=2x^2+2x+15x-3x^2-7x+35
=-x^2+10x+35

a: Ta có: \(\left(x+5\right)^2-4x\left(2x+3\right)^2-\left(2x-1\right)\left(x+3\right)\left(x-3\right)\)
\(=x^2+10x+25-4x\left(4x^2+12x+9\right)-\left(2x-1\right)\left(x^2-9\right)\)
\(=x^2+10x+25-16x^3-48x^2-36x-2x^3+18x+x^2-9\)
\(=-18x^3-46x^2-8x+16\)

\(a,2\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2+\left(x+1\right)^2\)
\(=2\left(x^2-1\right)+x^2-2x+1+x^2+2x+1\)
\(=2x^2-2+2x^2+2=4x^2\)
\(b,\left(x-y+1\right)^2+\left(1-y\right)^2+2\left(x-y+1\right)\left(y-1\right)\)
\(=\left(x-y+1\right)^2+2\left(x-y+1\right)\left(y-1\right)+\left(y-1\right)^2\)
\(=\left[\left(x-y+1\right)+\left(y-1\right)\right]^2\)
\(=\left[x-y+1+y-1\right]^2=x^2\)
đề cuối phải sửa cái cuối thành \(\left(3x+5\right)^2\)
\(c,\left(3x+1\right)^2-2\left(3x+1\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left[\left(3x+1\right)-\left(3x+5\right)\right]^2=\left[3x+1-3x-5\right]^2=16\)