Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khẳng định nào sau đây đúng A. B. C. ...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khẳng định nào sau đây đúng
A. 
B. 
C. 
D. 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 3 2018
Chọn A.
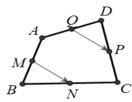
+ Do M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC .
suy ra MN // AC và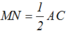 
(1).
+ Tương tự QP là đường trung bình của tam giác ADC
suy ra QP // AC và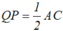 
(2).
+ Từ (1) và (2) suy ra MN // QP và MN = PQ do đó tứ giác MNPQ là hình bình hành
Vậy ta có 
CM
30 tháng 3 2019
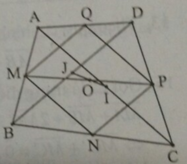
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D
CM
5 tháng 4 2019
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN.
Khi đó M N → = Q P →
Đáp án D
CM
18 tháng 10 2017
Tứ giác DMCK có hai đường chéo cắt nhau tại trung điểm mỗi đường (N là trung điểm của MK và CD). Do đó, tứ giác DMCK là hình bình hành.
Theo quy tắc hình bình hành ta có:
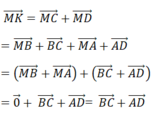
Đáp án B
+Do M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC