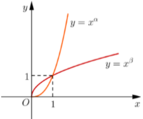
Cho α , β là các số thực. Đồ thị các hàm số y = x α , y = x β trên khoảng 0 ; + ∞ được cho hình vẽ bên. Khẳng định nào sau đây đúng?
A. 0 < β < 1 < α
B. β < 0 < 1 < α
C. 0 < α < 1 < β
D. α < 0 < 1 < β
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Hàm số x α nghịch biến do đó 0 < α < 1 .
Các hàm số x β , x γ là các hàm số đồng biến do đó β , γ > 1 .
Cho x = 100 ⇒ 100 β > 100 γ ⇒ β > γ .

Đáp án D
Với x > 1 mà lim x α = 0 ⇔ 0 < a < 1 và cũng suy ra β , γ > 1
Với x > 1 , với cùng 1 giá trị x 0 thì x β > x γ ⇒ β > γ .

a) - Với hàm số y = x + 1
Cho x = 0 y = 1 được A(0; 1)
Cho y = 0 x = -1 được B(-1; 0)
Nối A, B được đường thẳng y = x + 1
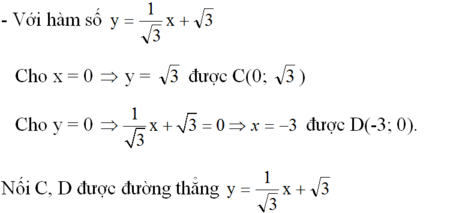
- Với hàm số y = √3 x - √3
Cho x = 0 => y = -√3 được E(0; -√3)
Cho y = 0 => x = 1 được F(1; 0).
Nối E, F được đường thẳng y = √3 x - √3
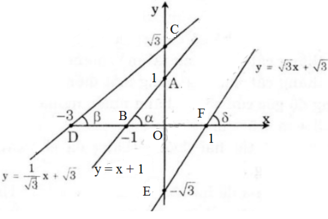
b) Ta có:
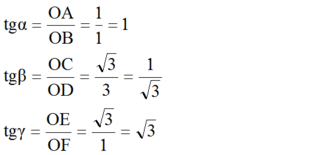
Suy ra α = 45o, β = 30o, γ = 60o

Điều kiện xác định: β ≥ 2
Yêu cầu của bài toán đưa đến giải bất phương trình 1 2 ≤ sin 2 α ≤ 1
Kết luận: π 12 + k π ≤ α ≤ 5 π 12 + kπ , k ∈ ℤ và β ≥ 2
Chọn B.
Chọn D.
Với x0 > 1 ta có:
Mặt khác, dựa vào hình dáng đồ thị ta suy ra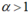 và
và