Biết rằng phương trình 3 + 5 2 + 3 3 - 5 2 = 2 x + 2 có hai nghiệm phân biệt là x 1 > x 2 . Nghiệm x 1 có dạng log a + b 5 2 9 , với a; b nguyên dương. Tính S = a4 + 10ab
A. 2611
B. 2681
C. 2422
D. 2429
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3
Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ó x – 1 = 0 ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B

Bài làm :
a) Thay m=-5 vào PT ; ta được :
\(x^2-2x-8=0\)
\(\Delta'=\left(-1\right)^2-1.\left(-8\right)=9>0\)
=> PT có 2 nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{1+\sqrt{9}}{1}=4\\x_2=\frac{1-\sqrt{9}}{1}=-2\end{cases}}\)
b) Đk để PT có 2 nghiệm phân biệt :
\(\Delta'>0\Leftrightarrow\left(-1\right)^2-1.\left(m-3\right)=1-m+3=4-m>0\)
\(\Rightarrow m< 4\)
Khi đó ; theo hệ thức Vi-ét ; ta có :
\(\hept{\begin{cases}x_1+x_2=2\left(1\right)\\x_1x_2=m-3\end{cases}}\)
Mà :
\(x_1=3x_2\Rightarrow x_1-3x_2=0\left(2\right)\)
Từ (1) và (2) ; ta có HPT :
\(\hept{\begin{cases}x_1+x_2=2\\x_1-3x_2=0\end{cases}}\Rightarrow\hept{\begin{cases}x_1=\frac{3}{2}\\x_2=\frac{1}{2}\end{cases}}\)
\(\Rightarrow x_1x_2=\frac{3}{4}\Rightarrow m=\frac{3}{4}+3=\frac{15}{4}\left(TMĐK\right)\)
Vậy m=15/4 thì ...
a,x\(^2\)-2x+m-3=0 (*)
thay m=-5 vào pt (*) ta đk:
x\(^2\)-2x+(-5)-3=0⇔x\(^2\)-2x-8=0
Δ=(-2)\(^2\)-4.1.(-8)=36>0
⇒pt có hai nghiệm pb
\(x_1=\dfrac{2+\sqrt{36}}{2}=4\) , \(x_2=\dfrac{2-\sqrt{36}}{2}=-2\)
vậy pt đã cho có tập nghiệm S=\(\left\{4;-2\right\}\)
b,\(x^2-2x+m-3=0\) (*)
Δ=(-2)\(^2\)-4.1.(m-3)=4-4m+12=16-4m
⇒pt luôn có hai nghiệm pb⇔Δ>0⇔16-4m>0⇔16>4m⇔m<4
với m<4 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)
theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=m-3\end{matrix}\right.\) (1) ,(2)
\(x_1,x_2\) TM \(x_1=3x_2\) (3)
từ (1) và (3) ta đk:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2+x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_2=2\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=3x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1}{2}\\x_1=\dfrac{3}{2}\end{matrix}\right.\)
thay \(x_1=\dfrac{3}{2},x_2=\dfrac{1}{2}\) vào (2) ta đk:
\(\dfrac{3}{2}.\dfrac{1}{2}=m-3\Leftrightarrow3=4m-12\Leftrightarrow4m=15\Leftrightarrow m=\dfrac{15}{4}\) (TM)
vậy m=\(\dfrac{15}{4}\) thì pt (*) có hai nghiệm pb \(x_1,x_2\) TMĐK \(x_1=3x_2\)

a)PT có 2 nghiệm phân biệt
`<=>Delta>0`
`<=>(2m+3)^2+4(2m+4)>0`
`<=>4m^2+12m+9+8m+16>0`
`<=>4m^2+20m+25>0`
`<=>(2m+5)^2>0`
`<=>m ne -5/2`
b)Áp dụng vi-ét:
$\begin{cases}x_1+x_2=2m+3\\x_1.x_2=-2m-4\\\end{cases}$
`|x_1|+|x_2|=5`
`<=>x_1^2+x_2^2+2|x_1.x_2|=25`
`<=>(x_1+x_2)^2+2(|x_1.x_2|-x_1.x_2)=25`
`<=>(2m+3)^2+2[|-2m-4|-(-2m-4)]=25`
Với `-2m-4>=0<=>m<=-2`
`=>pt<=>(2m+3)^2-25=0`
`<=>(2m-2)(2m+8)=0`
`<=>(m-1)(m+4)=0`
`<=>` $\left[ \begin{array}{l}x=1\\x=-4\end{array} \right.$
`-2m-4<=0=>m>=-2=>|-2m-4|=2m+4`
`<=>4m^2+12m+9+8m+16=25`
`<=>4m^2+20m=0`
`<=>m^2+5m=0`
`<=>` \left[ \begin{array}{l}x=0\\x=-5\end{array} \right.$
Vậy `m in {0,1,-4,-5}`

* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-
Chọn A.
Ta có
Phương trình đã cho thành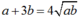
đây là phương trình đẳng cấp, ta có thể chia cả hai vế cho b > 0 như sau:
+) TH1.

+) TH2.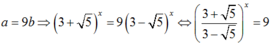

Do đó