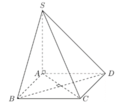
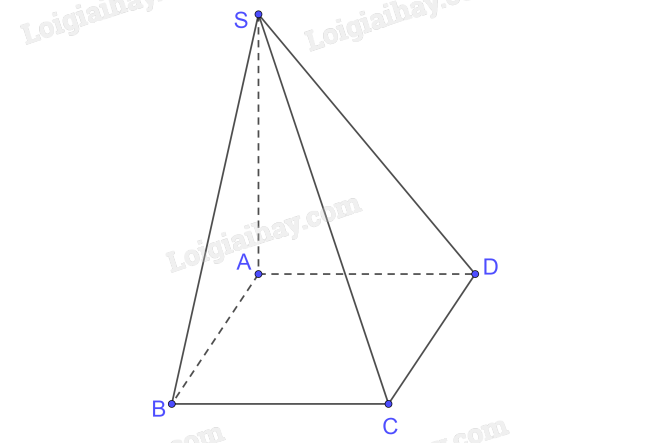
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật; AB=a,AD=2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
A. R = 3 a 2 2
B. R = 2 a 2 3
C. R = 2 a 3 3
D. R = 3 a 3 2


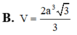


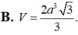
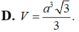
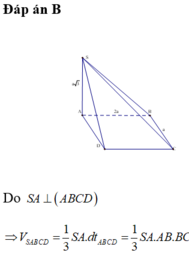
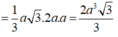
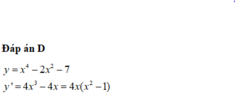


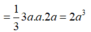

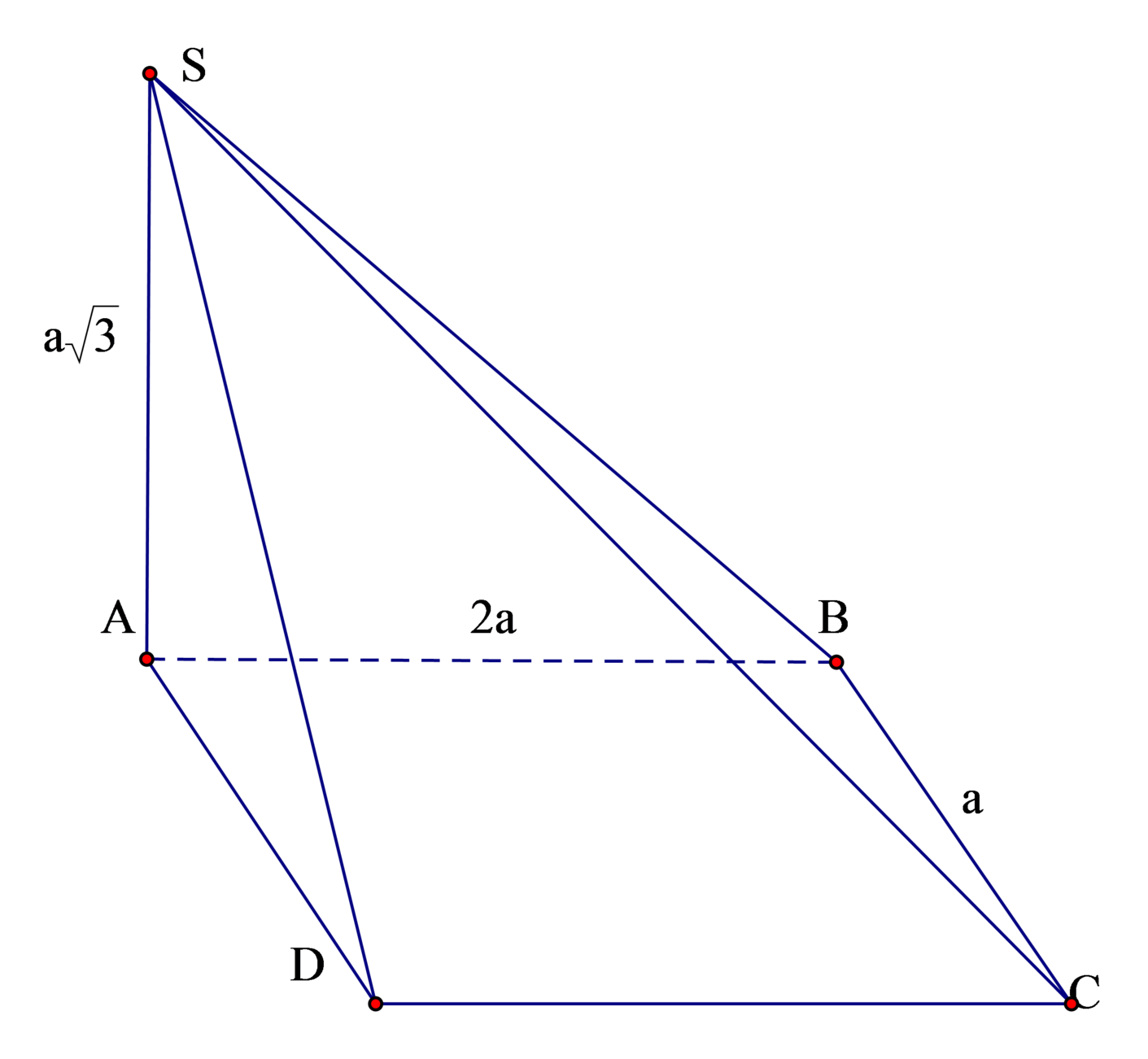
Đáp án đúng : C