Cho hình hộp chữ nhật ABCD.A′B′C′D′ có các cạnh A B = a , A D = 2 a , A A ' = 3 a . Tìm bán kính của mặt cầu ngoại tiếp tứ diện CB′C′D′.
A. 3 a 2 .
B. 14 a 2 .
C. 3 a
D. 7 a 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tâm mặt cầu ngoại tiếp hình hộp chính là tâm đối xứng của hình hộp, tâm đối xứng của hình hộp là trung điểm AC'
\(r=\frac{\sqrt{a^2+b^2+c^2}}{2}\)

Đáp án A
Vì qua 4 điểm không đồng phẳng tồn tại duy nhất mặt cầu do vậy mặt cầu ngoại tiếp tứ diện A B ' C D ' chính là mặt cầu ngoại tiếp hình chữ nhật ABCD.A'B'C'D'
⇒ R = A C ' 2 = A B 2 + A D 2 +AA ' 2 2 = a 14 2

Chọn đáp án C
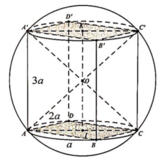
Mặt cầu ngoại tiếp tứ diện ACB’D’ cũng là mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’.
Bán kính mặt cầu là:
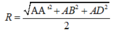
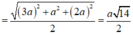

Chọn đáp án C
Mặt cầu ngoại tiếp tứ diện ACB’D’ cũng là mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’.
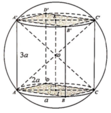
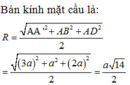

Chọn đáp án C
Bán kính r của mặt cầu ngoại tiếp hình hộp chữ nhật có ba kích thước a, b, c được tính theo công thức

Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
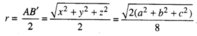
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có V ABCD = V OABC + V OBCD + V OCDA + V ODAB
= 4 V OABC = 4 r ' S ABC / 3
Do đó:
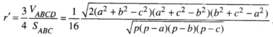
Trong đó 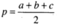

∠ BAC = 120 ° và b = c, khi đó ABC là một tam giác cân có góc A ở đỉnh bằng 120 ° và cạnh bên bằng b. Gọi M là trung điểm của cạnh BC. Kéo dài AM một đoạn MK = AM, ta có KA = KB = KC = AB = AC = b.
Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại K. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có: OS = OA = OB = OC và
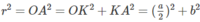
Do đó ta có mặt cầu tâm O ngoại tiếp tứ diện và có bán kính
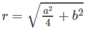
Đáp án B
Gọi M là trung điểm của B′D′,I là giao điểm của đường trung trực của CC′ và IM.
Dễ thấy I là tâm mặt cầu ngoại tiếp chóp CC′B′D′.
Ta có
R = I D ' = I M 2 + M D ' 2 = C C ' 2 4 + B ' D ' 2 4 = 9 a 2 + 4 a 2 + a 2 4 = 14 a 2 .