Làm tính chia:
a) 22 x 4 y 2 z : 5 x 2 y ; b) x 6 y 7 zt : x 6 y 7 ;
c) ( - 5 x ) 3 y 2 z 2 : 15 x 3 y ; d) 3 8 ( xy 2 ) 5 : − 1 2 x 2 y 2 ;
e) ( - x 3 y 6 z 9 ) 10 : ( xyz ) 15 ; g) ( x - 1 ) 6 : ( x 2 - 2 x + l ) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

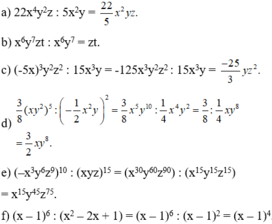

\(a,=5^3:5^2=5\\ b,=\left(\dfrac{3}{4}\right)^{5-3}=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\\ c,=1728-512=1216\\ d,=x^{10}:x^8=x^2\\ e,=\left(-x\right)^{5-3}=\left(-x\right)^2=x^2\\ f,=\left(-y\right)^{5-4}=-y\)

`a, (4x^3y^2 - 8x^2y + 10xy) : 2xy`
`= 2x^2y - 4x + 5`.
`b, 7x^4y^2 - 2x^2y^2 - 5x^3y^4 : 3x^2y`
`= 7/3 x^2y - 3/2y - 5/3xy^3`

`a, 20x^3y^5 : 5x^2y^2`
`= (20:5)x^(3-2) . y^(5-2)`
`= 4xy^3`
`b, 18x^3y^5 : (3(-x^3)y^2)`
`= -(18:3)y^(5-3)`
`= -6y^2`

Thực hiện phép chia:
a) (-y^2):y^4=\(\dfrac{-1}{y^2}\)
b) (-x)^5:(-x)^3=(-x)^2
a) (-y2) : y4=\(\dfrac{-1}{y^2}\)
b) (-x)5 : (-x)3 = (-x)2

\(\dfrac{x}{y}=\dfrac{2}{5}\rightarrow\dfrac{x}{2}=\dfrac{y}{5}\)
\(\dfrac{y}{z}=\dfrac{5}{3}\rightarrow\dfrac{y}{5}=\dfrac{z}{3}\)
Ta có: \(\dfrac{x}{2}=\dfrac{y}{5},\dfrac{y}{5}=\dfrac{z}{3}\rightarrow\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{3}\rightarrow\dfrac{2x}{4}=\dfrac{y}{5}=\dfrac{3z}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/4=y/5=(3z)/9=(2x-y+3z)/(4-5+9)=16/8=2`
`-> x/2=y/5=z/3=2`
`-> x=2*2=4, y=2*5=10, z=2*3=6`
`x/5=y/3 -> x/25=y/15`
`y/5=z/4 -> y/15=z/12`
`x/25=y/15, y/15=z/12`
`-> x/25=y/15=z/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/25=y/15=z/12=(x-y+z)/(25-15+12)=22/22=1`
`-> x/25=y/15=z/12=1`
`-> x=25, y=15, z=12`
a: x/y=2/5
=>x/2=y/5
y/z=5/3
=>y/5=z/3
=>x/2=y/5=z/3
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{3}=\dfrac{2x-y+3z}{2\cdot2-5+3\cdot3}=\dfrac{16}{8}=2\)
=>x=4; y=10; z=6
b: x/5=y/3
=>x/25=y/15
y/5=z/4
=>y/15=z/12
=>x/25=y/15=z/12
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{25}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y+z}{25-15+12}=1\)
=>x=25; y=15; z=12

5: Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
nên x=5k; y=3k
Ta có: \(x^2-y^2=4\)
\(\Leftrightarrow25k^2-9k^2=4\)
\(\Leftrightarrow k^2=\dfrac{1}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\pm\dfrac{5}{4}\\y=\pm\dfrac{3}{4}\end{matrix}\right.\)

Các phần còn lại check lại đề bài.
b) Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+z}{2+4}=\frac{18}{6}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=3\Rightarrow x=6\\\frac{y}{3}=3\Rightarrow y=9\\\frac{z}{4}=3\Rightarrow z=12\end{cases}}\)
d) Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{x+1}{3}=\frac{y+2}{4}=\frac{z+3}{5}=\frac{x+y+z+6}{3+4+5}=\frac{24}{12}=2\)
\(\Rightarrow\hept{\begin{cases}x+1=6\\y+2=8\\z+3=10\end{cases}}\Rightarrow\hept{\begin{cases}x=5\\y=6\\z=7\end{cases}}\)

Bài làm:
Ta có: \(\frac{x}{3}=\frac{y}{5}\Leftrightarrow\frac{x}{6}=\frac{y}{10}\)(1)
Và \(\frac{y}{2}=\frac{z}{4}\Leftrightarrow\frac{y}{10}=\frac{z}{20}\) (2)
Từ (1) và (2) => \(\frac{x}{6}=\frac{y}{10}=\frac{z}{20}\Leftrightarrow\frac{x}{3}=\frac{y}{5}=\frac{z}{10}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{10}=\frac{-2x+y-z}{-6+5-10}=\frac{-22}{-11}=2\)
=> \(\hept{\begin{cases}x=6\\y=10\\z=20\end{cases}}\)
Theo bài ra ta có : \(\frac{x}{3}=\frac{y}{5}\Leftrightarrow\frac{x}{6}=\frac{y}{10}\)(*)
\(\frac{y}{2}=\frac{z}{4}\Leftrightarrow\frac{y}{10}=\frac{z}{20}\)(**)
Từ (*) ; (**) ta có : \(\frac{x}{6}=\frac{y}{10}=\frac{z}{20}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có
\(\frac{x}{6}=\frac{y}{10}=\frac{z}{20}=\frac{-2x+y-z}{-2.6+10-20}=-\frac{22}{-22}=1\)
: \(x=6;y=10;z=20\)