Giải phương trình: 2 x + 3 3 x + 8 2 - 7 x + 1 = x - 5 3 x + 8 2 - 7 x + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ĐKXĐ: \(x\ne1\)
Ta có: \(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)
\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow21x-2x=-2+9\)
\(\Leftrightarrow19x=7\)
\(\Leftrightarrow x=\dfrac{7}{19}\)
Vậy: \(S=\left\{\dfrac{7}{19}\right\}\)

a) ĐKXĐ: \(x\notin\left\{-1;0\right\}\)
Ta có: \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x+1\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}\)
Suy ra: \(x^2+3x+x^2-3x+2=2x^2+2x\)
\(\Leftrightarrow2x^2+2-2x^2-2x=0\)
\(\Leftrightarrow-2x+2=0\)
\(\Leftrightarrow-2x=-2\)
hay x=1(nhận)
Vậy: S={1}
b) ĐKXĐ: \(x\notin\left\{-7;\dfrac{3}{2}\right\}\)
Ta có: \(\dfrac{3x-2}{x+7}=\dfrac{6x+1}{2x-3}\)
\(\Leftrightarrow\left(3x-2\right)\left(2x-3\right)=\left(6x+1\right)\left(x+7\right)\)
\(\Leftrightarrow6x^2-9x-4x+6=6x^2+42x+x+7\)
\(\Leftrightarrow6x^2-13x+6-6x^2-43x-7=0\)
\(\Leftrightarrow-56x-1=0\)
\(\Leftrightarrow-56x=1\)
hay \(x=-\dfrac{1}{56}\)(nhận)
Vậy: \(S=\left\{-\dfrac{1}{56}\right\}\)
c) ĐKXĐ: \(x\ne-\dfrac{2}{3}\)
Ta có: \(\dfrac{5}{3x+2}=2x-1\)
\(\Leftrightarrow5=\left(3x+2\right)\left(2x-1\right)\)
\(\Leftrightarrow6x^2-3x+4x-2-5=0\)
\(\Leftrightarrow6x^2+x-7=0\)
\(\Leftrightarrow6x^2-6x+7x-7=0\)
\(\Leftrightarrow6x\left(x-1\right)+7\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(6x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\6x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{7}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{7}{6}\right\}\)
d) ĐKXĐ: \(x\ne\dfrac{2}{7}\)
Ta có: \(\left(2x+3\right)\cdot\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)
\(\Leftrightarrow\left(2x+3\right)\cdot\left(\dfrac{3x+8+2-7x}{2-7x}\right)-\left(x-5\right)\left(\dfrac{3x+8+2-7x}{2-7x}\right)=0\)
\(\Leftrightarrow\left(2x+3-x+5\right)\cdot\dfrac{-4x+6}{2-7x}=0\)
\(\Leftrightarrow\left(x+8\right)\cdot\left(-4x+6\right)=0\)(Vì \(2-7x\ne0\forall x\) thỏa mãn ĐKXĐ)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\-4x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\-4x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\left(nhận\right)\\x=\dfrac{3}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{-8;\dfrac{3}{2}\right\}\)

\(\dfrac{1}{x+2}+\dfrac{6x+12}{x^3+8}-\dfrac{7}{x^2-2x+4}=0\) \(\left(đk:x\ne-2\right)\)
\(\Leftrightarrow\dfrac{x^2-2x+4+6x+12-7\left(x+2\right)}{x^3+8}=0\)
\(\Leftrightarrow\dfrac{x^2-3x+2}{x^3+8}=0\)
\(\Leftrightarrow x^2-3x+2=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)-\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)(TM)
Vậy ...
dk : x khac -2
\(\Rightarrow x^2-2x+4+6x+12-7\left(x+2\right)=0\)
\(\Leftrightarrow x^2+4x+16-7x-14=0\Leftrightarrow x^2-3x+2=0\)
\(\Leftrightarrow x^2-2x-x+2=0\Leftrightarrow x\left(x-2\right)-\left(x-2\right)=0\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\Leftrightarrow x=1;x=2\)

c.
\(\Leftrightarrow x^2+3-\left(3x+1\right)\sqrt{x^2+3}+2x^2+2x=0\)
Đặt \(\sqrt{x^2+3}=t>0\)
\(\Rightarrow t^2-\left(3x+1\right)t+2x^2+2x=0\)
\(\Delta=\left(3x+1\right)^2-4\left(2x^2+2x\right)=\left(x-1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{3x+1-x+1}{2}=x+1\\t=\dfrac{3x+1+x-1}{2}=2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+3}=x+1\left(x\ge-1\right)\\\sqrt{x^2+3}=2x\left(x\ge0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3=x^2+2x+1\left(x\ge-1\right)\\x^2+3=4x^2\left(x\ge0\right)\end{matrix}\right.\)
\(\Leftrightarrow x=1\)
a.
Đề bài ko chính xác, pt này ko giải được
b.
ĐKXĐ: \(x\ge-\dfrac{7}{2}\)
\(2x+7-\left(2x+7\right)\sqrt{2x+7}+x^2+7x=0\)
Đặt \(\sqrt{2x+7}=t\ge0\)
\(\Rightarrow t^2-\left(2x+7\right)t+x^2+7x=0\)
\(\Delta=\left(2x+7\right)^2-4\left(x^2+7x\right)=49\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{2x+7-7}{2}=x\\t=\dfrac{2x+7+7}{2}=x+7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+7}=x\left(x\ge0\right)\\\sqrt{2x+7}=x+7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-7=0\left(x\ge0\right)\\x^2+12x+42=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=1+2\sqrt{2}\)

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) đẻ được hỗ trợ tốt hơn. Viết như thế kia rất khó đọc => khả năng bị bỏ qua bài cao.
a: =>3x=3
=>x=1
b: =>12x-2(5x-1)=3(8-3x)
=>12x-10x+2=24-9x
=>2x+2=24-9x
=>11x=22
=>x=2
c: =>2x-3(2x+1)=x-6x
=>-5x=2x-6x-3=-4x-3
=>-x=-3
=>x=3
d: =>2x-5=0 hoặc x+3=0
=>x=5/2 hoặc x=-3
e: =>x+2=0
=>x=-2

a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27
a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27

Câu 1 :
a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)
\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)
\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)
Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)
tương tự
\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)
\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)
\(< =>95-24x+40=6-4x-15x+5\)
\(< =>-24x+135=-19x+11\)
\(< =>5x=135-11=124\)
\(< =>x=\frac{124}{5}\)

a) \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)=8\)
\(\Leftrightarrow x\left(x+3\right)\left(x+1\right)\left(x+2\right)=8\)
\(\Leftrightarrow\left(x^2+3x\right)\left(x^2+3x+2\right)=8\)
Đặt \(x^2+3x=u\)
Phương trình trở thành: \(u\left(u+2\right)=8\)
\(\Leftrightarrow u^2+2u-8=0\Leftrightarrow\left(u-2\right)\left(u+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}u-2=0\\u+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}u=2\\u=-4\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+3x=2\\x^2+3x=-4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2+3x-2=0\\x^2+3x+4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\pm\frac{\sqrt{17}}{2}-1\frac{1}{2}\\x\in\varnothing\end{cases}}\)
c) \(\left(x+2\right)\left(x+3\right)\left(x-7\right)\left(x-8\right)=144\)
\(\Leftrightarrow\left(x+2\right)\left(x-7\right)\left(x+3\right)\left(x-8\right)=144\)
\(\Leftrightarrow\left(x^2-5x-14\right)\left(x^2-5x-24\right)=144\)
Đặt \(x^2-5x-14=v\)
Phương trình trở thành: \(v\left(v-10\right)=144\)
\(\Leftrightarrow v^2-10v-144=0\Leftrightarrow\left(v-18\right)\left(v+8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}v-18=0\\v+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}v=18\\v=-8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-5x-14=18\\x^2-5x-14=-8\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm\frac{3\sqrt{17}}{2}+\frac{5}{2}\\x\in\left\{6;-1\right\}\end{cases}}\)

a: 5-3x=6x+7
=>-3x-6x=7-5
=>-9x=2
=>\(x=-\dfrac{2}{9}\)
b: \(\dfrac{3x-2}{6}-5=3-\dfrac{2\left(x+7\right)}{4}\)
=>\(\dfrac{3x-2}{6}+\dfrac{x+7}{2}=8\)
=>\(\dfrac{3x-2+3\left(x+7\right)}{6}=8\)
=>3x-2+3x+14=48
=>6x+12=48
=>6x=36
=>\(x=\dfrac{36}{6}=6\)
c: \(\left(x-1\right)\left(5x+3\right)=\left(3x-8\right)\left(x-1\right)\)
=>\(\left(x-1\right)\left(5x+3\right)-\left(3x-8\right)\left(x-1\right)=0\)
=>(x-1)(5x+3-3x+8)=0
=>(x-1)(2x+11)=0
=>\(\left[{}\begin{matrix}x-1=0\\2x+11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{11}{2}\end{matrix}\right.\)
d: \(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
=>\(\left(2x-1-x-3\right)\left(2x-1+x+3\right)=0\)
=>\(\left(x-4\right)\left(3x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)

a: =>3,6-1,7x=2,3-1,4-4=0,9-4=-3,1
=>1,7x=6,7
hay x=67/17
b: \(\Leftrightarrow30\left(5x+4\right)-15\left(3x+5\right)=24\left(4x+9\right)-40\left(x-9\right)\)
=>150x+120-45x-75=96x+216-40x+360
=>105x+45=56x+576
=>49x=531
hay x=531/49
Điều kiện xác định: x ≠ 2/7.
Suy ra: 10 – 4x = 0 ⇔ x = 5/2 (thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm là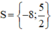
1029wieru56473892211984275678