Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
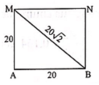
+ Bước sóng của sóng trên: 
+ Dựa vào định lí Pytago ta tính nhanh được:
+ Hiệu đường đi của sóng tại B:
+ Hiệu đường đi của sóng tại M:
+ Hai nguồn dao động ngược pha nên số cực đại trên BM thỏa mãn:
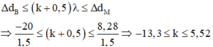
Có 19 giá trị k thỏa mãn nên có 19 cực đại trên BM
Đáp án C
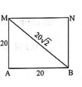
+ Bước sóng của sóng trên: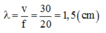 
+ Dựa vào định lí Pytago ta tính nhanh được:
+ Hiệu đường đi của sóng tại B:
+ Hiệu đường đi của sóng tại M:
+ Hai nguồn dao động ngược pha nên số cực đại trên BM thỏa mãn:
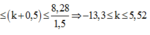
Có 19 giá trị k thỏa mãn nên có 19 cực đại trên BM
Chọn đáp án D
Một Hypybol cực đại sẽ cắt AB tại hai điểm đường thẳng CD tại 2 điểm (trừ trường hợp hypybol cắt C tại 1 điêm). Vì trên d có 13 điểm đao động với biên độ cực đại và A C < A B 2 nên C là điểm thuộc cực đại bậc xa trung tâm nhất sẽ thuộc cực đại bậc 7.
Do đó ta có 7 λ = d 2 − d 1 ⇔ 7 λ = 26 − 4 , 6 − 4 , 6 ⇒ λ = 2 , 4 c m
Tốc độ truyền sóng là v = λ f = 2 , 4.25 = 60 c m
Đáp án: A
HD Giải: λ = 300 50 = 6cm
Số điểm dao động với biên độ cực đại, ta có:
-AB < kλ < AB
<=> -20 < 6k < 20
<=> - 3,3 < k < 3,3
Suy ra trên AB có 7 cực đại
$\lambda = \dfrac{3}{2}$
Vị trí cực đại thoả mãn: $(20-20\sqrt {2} \le (k+0,5)\lambda \le 20 \Rightarrow $ số $k=19$
Vậy có 19 điểm dao động biên độ cực đại trên đoạn AD.
Chọn đáp án D.
Không mất tính tổng quát giả sử λ = 1.
Ta có:
Vì trên AB có 11 vị trí cực đại nên suy ra 5 < λ < 6.
(Dựa vào các đáp án suy ra chỉ có 5,3λ thỏa mãn).
. 
Đáp án: B
HD Giải:
Hai nguồn đồng pha nên điểm dao động với biên độ cực đại thỏa mãn:
d2 – d1 = k.λ
Số điểm dao động với biên độ cực đại trên đoạn CD thỏa mãn:
<=>
<=>
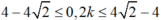
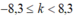
có 17 cực đại