cho hs y= x3/3-2x2+3x+2/3 tọa độ điểm cực đjai của đt hàm số là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2018
Đáp án D.
Tập xác định D = R.
Ta có y’ = x2 – 4x + 3, y’ = 0
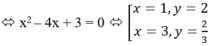
Bảng biến thiên
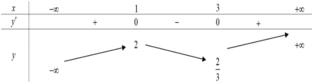
Tọa độ điểm cực đại của hàm số là (1;2).
CM
22 tháng 7 2019
Chọn D
+ T a c ó : y ' = 3 x 2 - 4 x + 1
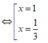
Hàm số đạt cực tiểu tại x = 1 ⇒ y C T = 3
PT
1
CM
10 tháng 12 2018
Đáp án D
Ta có y ' = 3 x 2 - 3 ⇒ y ' ' = 6 x , y ' = 0 ⇔ x = ± 1 → y ' ' 1 > 0 y ' ' - 1 < 0 ⇒ hàm số đạt cực tiểu tại x = 1. ⇒ Điểm cực tiểu A(1;0)
CM
11 tháng 1 2018
Đáp án D
Ta có
Mặt khác
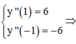
Tọa độ cực tiểu của đồ thị hàm số là (1;0)
CM
24 tháng 12 2019
Chọn B.
Do đó hàm số có cực đại là (1;2), cực tiểu là 3 ; 2 3 .
CM
23 tháng 9 2018
Đáp án là C
• Hàm số (I) là hàm nhất biến nên không có cực trị.
• Hàm số (II) có phương trình y'=2 có 2 nghiệm phân biệt nên có 2 cực trị.
Hàm số (III) có a.b=-2<0 nên có 3 cực trị.
CM
13 tháng 9 2019
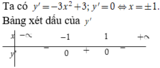
Từ đó suy ra hàm số đạt cực tiểu tại x 1 = 1, đạt cực đại tại x 2 = -1
Suy ra S = x 1 + 2 x 2 = -1
Chọn A.
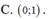
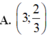
\(y'=x^2-4x+3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(\Rightarrow\) Tọa độ điểm cực đại là \(\left(1;2\right)\)