Tính tổng T tất cả các nghiệm của phương trình 4 x - 8 . 2 x + 4 = 0
A. T = 1
B. T = 2
C. T = 8
D. T = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KD
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 6 2020
\(\Leftrightarrow\left(x^2-3x+3\right)^2-5\left(x^2-3x+3\right)+4=0\)
Đặt \(x^2-3x+3=t\)
\(\Rightarrow t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-3x+3=1\\x^2-3x+3=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x+2=0\\x^2-3x-1=0\end{matrix}\right.\)
Theo Viet, tổng các nghiệm: \(x_1+x_2+x_3+x_4=3+3=6\)
. Tính tổng T=a+b
CM
12 tháng 3 2017
Đáp án D
→
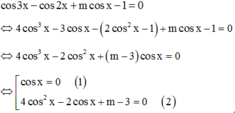
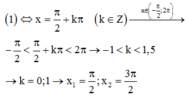
(1) có 2 nghiệm thuộc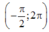 
Để phương trình có đúng 8 nghiệm thuộc khoảng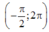
thì (2) phải có đúng 6 nghiệm phân biệt thuộc
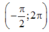và khác
x
1
;
x
2
Đặt t = cos x ( - 1 ≤ x ≤ 1 ) , (2) trở thành f ( t ) = 4 t 2 - 2 t + m - 3 = 0 ( 3 )
+ Nếu
0
<
t
<
1
thì phương trình cosx=t có 3 nghiệm phân biệt thuộc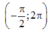
+ Nếu
-
1
<
t
<
0
thì phương trình cosx=t có 2 nghiệm phân biệt thuộc khoảng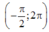
Do đó (2) có đúng 6 nghiệm phân biệt thuộc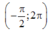
⇔ (3) có 2 nghiệm t 1 ; t 2 thỏa mãn 0 < t 1 < t 2 < 1
9 tháng 5 2022
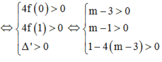
a, Ta có a + b + c = 1 + 5 - 6 = 0
Vậy pt có 2 nghiệm x = 1 ; x = -6
b, \(x^2-2mx+4m-4=0\)
\(\Delta'=m^2-4m+4=\left(m-2\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4m-4\end{matrix}\right.\)
\(\left(x_1+x_2\right)^2-2x_1x_2-8=0\)
\(\Leftrightarrow4m^2-2\left(4m-4\right)-8=0\Leftrightarrow4m^2-8m=0\Leftrightarrow m=0;m=2\)
12 tháng 5 2022
a) \(x^2+5x-6\) = 0
Ta có: a + b + c = 1 + 5 + ( - 6 ) = 0
⇔ \(\left\{{}\begin{matrix}x_1=1\\x_2=-6\end{matrix}\right.\)
Vậy S = \(\left\{1;-6\right\}\)
b) \(x^2-2mx+4m-4=0\)
Δ' = \(\left(-m\right)^2\) - ( 4m - 4 )
Δ' = \(m^2\) - 4m +4
\(\left(m-2\right)^2\ge0\forall m\ne2\)
Vậy phương trình luôn có 2 nghiệm
* Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4m-4\end{matrix}\right.\)
* Theo đề bài : \(x_1^2+x_2^2-8=0\)
⇔ \(\left(x_1+x_2\right)^2-2x_1x_2-8=0\)
⇒ \(\left(2m\right)^2\)- 2.( 4m - 4 ) - 8 = 0
⇔ \(4m^2\) - 8m + 8 - 8 = 0
⇔ \(4m^2\) - 8m = 0
⇔ 4m.( m - 2 ) = 0
⇔ \(\left[{}\begin{matrix}4m=0\\m-2=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}m=0\left(thoảmãn\right)\\m=2\left(loại\right)\end{matrix}\right.\)
Vậy m = 0 thì t/m đề bài
Chọn B