Một hình trụ tròn xoay bán kính đáy bằng R, trục O ' O = R 6 . Một đoạn thẳng A B = R 2 với A ∈ O và B ∈ O . Tính góc giữa AB và trục hình trụ.
A. 30 o
B. 45 o
C. 60 o
D. 75 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

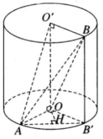
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2

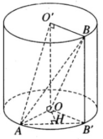
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là 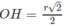

Chọn đáp án D
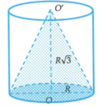
Diện tích xung quanh của hình trụ là
S 1 = 2 πRh = 2 πR 2 3 đvđt
Đường sinh của hình nón là
![]()
Diện tích xung quang của hình nón là
![]()
Vậy tỉ số diện tích xung quanh của hình trụ và hình nón là
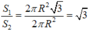

Chọn đáp án C.
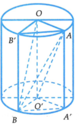
Kẻ các đường sinh AA', BB' của hình trụ (T).
Khi đó
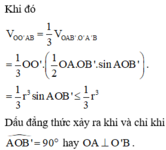
Như vậy, khối tứ diện có thể tích lớn nhất bằng
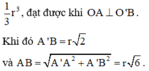
Kẻ đường sinh B'B. Khi đó B'B = O'O = R 6
Ta có
tan a = tan A B ' B ^ - A B B ' B = R 2 R 6 = 3 3 ⇒ α = 30 o
Đáp án A