Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
+ Áp dụng công thức
+ Vận tốc dài: 
+ Gia tốc hướng tâm:
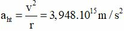
Một vật rắn đang quay đều quanh một trục cố định đi qua vật. Vận tốc dài của một điểm xác định trên vật rắn ở cách trục quay một khoảng \(r\ne0\) có độ lớn không thay đổi
Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)
A và B có cùng tốc độ góc \(\omega\)
\(r_A;r_B\) là bán kính quỹ đạo chuyển dộng tròn đều của A và B.
Ta có: \(r_A-r_B=40\) (1)
Tốc độ dài của A và B:
\(\left\{{}\begin{matrix}v_A=\omega\cdot r_A=1,2\\v_B=\omega\cdot r_B=0,4\end{matrix}\right.\)\(\Rightarrow r_A=3r_B\left(2\right)\)
Từ (1) và (2) ta suy ra: \(r_B=20cm\)
\(\omega=\dfrac{v_B}{r_B}=\dfrac{0,4}{20\cdot10^{-2}}=2\)rad/s
Chọn A.
Đáp án A