Trên trục O ; i → , cho ba điểm A; B; C lần lượt có tọa độ là -5; 2; 4. Tìm tọa độ điểm M thỏa mãn 2 M A → + 4 M B → + 3 M C → = 0 →
A. 10/3
B. -10/3
C. 10/9
D. 9/10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
25 tháng 5 2016
Điểm M có tọa độ 4,2 cm nên \(O'M=\sqrt{OM^2+O'O^2}=5,8cm\)
Do M dao động với biên độ cực tiểu và xa nguồn nhất nên
\(O'M-OM=\text{λ}\)
\(\Rightarrow\text{λ}=1,6cm\)
Từ đó tính được có 4 điểm dao động cực đại trên đoạn OO' nên có 2 điểm dao động cực đại trên đoạn ON (với N là trung điểm OO')
Mỗi đường hypebol qua điểm dao động cực đại trên đoạn ON cắt trục Ox tại 2 điểm
Vậy có 4 điểm dao động với biên độ cực đại trên Ox
MN
4 tháng 4 2021
a) Khoảng cách từ điểm O đến điểm A: 2 đơn vị.
b) Những điểm cách O một khoảng là 5 đơn vị là: điểm 5 và -5.
DT
Đỗ Thanh Hải
CTVVIP
4 tháng 4 2021
a) Khoảng cách từ điểm O đến điểm A = |0-(-2)| = 2
b) Các điểm cách O một khoảng 5 đơn vị là: -7 và 3
VT
12 tháng 8 2019
Chọn đáp án D.
Khi vật hướng lên thì ảnh hướng xuống, luôn ngược chiều với vật nên ảnh là ảnh thật, thấu kính là thấu kính hội tụ, độ phóng đại k < 0.
k = h ' h = − d ' d ⇔ − d ' d = − 6 4 = − 1 , 5 ⇒ d ' = 1 , 5 d = 1 , 5.30 = 45 c m
Tiêu cự f = d ' . d d ' + d = 45.30 45 + 30 = 18 c m
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a)
b) Ta có: Tọa độ các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) lần lượt là: -5; 5
Ta có \(\overrightarrow {AB} = - \overrightarrow {CD} \)
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng
VT
17 tháng 3 2018
Giải thích: Đáp án C
Phương pháp: Sử dụng công thức thấu kính và kĩ năng đọc đồ thị
Cách giải:
Ta có hệ số phóng đại ảnh qua thấu kính là k = - 0,5
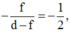thay d = 30cm
=> f = 10cm
Đáp án C