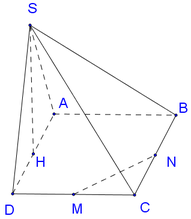
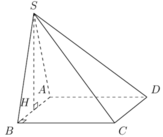
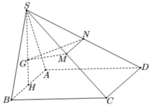
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây?
A . x 2 + 2 x y - y 2 > 160
B . x 2 - 2 x y + 2 y 2 < 109
C . x 2 + x y - y 4 < 145
D . x 2 - x y + y 4 > 125



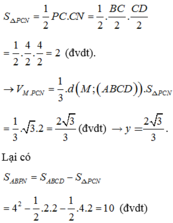




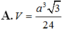
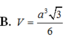
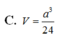
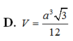



Đáp án C
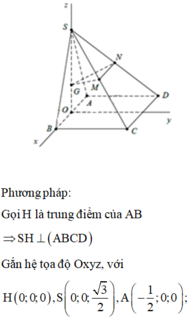
Gọi H là trung điểm của AB. Do ∆ SAB đều nên SH ⊥ AB và
Mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD).
Từ
Ta có
Lại có
* Phương án A:
* Phương án B:
* Phương án C:
* Phương án D: