Ai làm cho em được không...
Đọc tiếp
Ai làm cho em được không ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
1 tháng 3 2022
Lời giải:
$\Delta'=(m+1)^2-(2m-3)=m^2+4>0$ với mọi $m$ nên pt luôn có 2 nghiệm pb với mọi $m$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=2m-3$
Để $x_1<1<x_2$
$\Leftrightarrow (x_1-1)(x_2-1)<0$
$\Leftrightarrow x_1x_2-(x_1+x_2)+1<0$
$\Leftrightarrow 2m-3-2(m+1)+1<0$
$\Leftrightarrow -3-2+1<0$
$\Leftrightarrow -4<0$ (luôn đúng)
Vậy PT luôn có 2 nghiệm pb thỏa mãn đề với mọi $m\in\mathbb{R}$
28 tháng 2 2022
x2-(m-1)x+m-2=0(1)
Để phương trình có hai nghiệm phân biệt thì Δ=(-m+1)2-4(m-2)
=m2-2m+1-4m+8
=m2-6m+9
=(m-3)2≥0 với mọi m
⇒phương trình luôn có hai nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\begin{cases} x_1+x_2=m-2 \\ x_1.x_2=m-1 \end{cases}\)(2)
TH1:x1,x2 là hai cạnh góc vuông
⇒x1=x2
Từ (2)\(\begin{cases} x_1+x_1=m-2 \\ x_1^2=m-1 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_1=\frac{m-1}{2}\\ x_1=\sqrt{m-2} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{2}\)=\(\sqrt{m-2}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{4}\)=m-2
\(\Leftrightarrow\)m2-6m+9=0
\(\Leftrightarrow\)(m-3)2=0
\(\Leftrightarrow\)m=3
TH2:x1 là cạnh huyền,x2 là cạnh góc vuông
⇒x1=\(\sqrt{2}\)x2
Từ (2)⇒\(\begin{cases} \sqrt{2} x_2+x_2=m-1 \\ \sqrt{2} x_2^2=m-2 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_2= \frac{m-1}{1+\sqrt{2}} \\ x_2=\sqrt{\frac{m-2}{\sqrt{2}}} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{1+\sqrt{2}}\)=\(\sqrt{\dfrac{m-2}{\sqrt{2}}}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{3+2\sqrt{2}}\)=\(\dfrac{m-2}{\sqrt{2}}\)
\(\Leftrightarrow\)\(\left(3+2\sqrt{2}\right)\)\(m\)\(-6-2\sqrt{2}\)\(=\sqrt{2}m^2-2\sqrt{2}m+\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}m^2-\left(4\sqrt{2}+3\right)m+3\sqrt{2}+6=0\)
\(\Leftrightarrow\)rồi m bằng bao nhiêu thì tự giải nhé mệt r
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
\(\Delta=25-4\left(m-1\right)=29-4m>0\Rightarrow m< \dfrac{29}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\)
\(2x_1=\sqrt{x_2}\Rightarrow\left\{{}\begin{matrix}x_1;x_2\ge0\\4x_1^2=x_2=5-x_1\end{matrix}\right.\)
\(\Rightarrow4x_1^2+x_1-5=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-\dfrac{5}{4}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x_2=4x_1^2=4\)
Thế vào \(x_1x_2=m-1\Rightarrow m-1=4\Rightarrow m=5\)
L
19 tháng 5 2022
cẩn thận là được bạn ạ, có thể luyện tập dần đi cũng được, vẽ mấy hình trong sgk, sbt hay trên mạng cũng có á
7 tháng 12 2021
\(12,ĐK:x,y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{2}{y}=4\\\dfrac{6}{x}-\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x}=5\\\dfrac{2}{x}+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\left(tm\right)\)
\(13,\Leftrightarrow\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left(x+1\right)=22\\3\left(x+1\right)+2\left(x+2y\right)=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\6+2+4y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(14,ĐK:x+y\ne0;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}+\dfrac{1}{y-1}=5\\\dfrac{4}{x+y}-\dfrac{8}{y-1}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}-\dfrac{2}{y-1}=-1\\\dfrac{9}{y-1}=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\left(tm\right)\)
\(15,ĐK:x\ge-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-6\sqrt{x+1}=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x+1}=14\\2\left(x+y\right)+\sqrt{x+1}=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\left(tm\right)\\6+2y+2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\left(tm\right)\)
7 tháng 12 2021
\(16,ĐK:x\ne1;y\ne-2\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{4x}{x-1}+\dfrac{2}{y+2}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7x}{x-1}=14\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\left(tm\right)\)
\(17,ĐK:x\ge0;y\ge1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\8\sqrt{x}-2\sqrt{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\sqrt{x}=9\\\sqrt{x}+2\sqrt{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-1}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
\(18,\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\left|y+2\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\left[{}\begin{matrix}y=-1\\y=-3\end{matrix}\right.\end{matrix}\right.\\ 20,ĐK:y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{3}{y-1}=5\\12x-\dfrac{3}{y-1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=14\\2x+\dfrac{3}{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\dfrac{3}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\left(tm\right)\)
\(21,ĐK:x\ne-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=19\\\dfrac{3}{x+1}-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\3-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\left(tm\right)\)
TN
26 tháng 4 2017
Đầu tiên, họ(thằng ra đề) đưa ra giả thuyết và kết luận
vd: Cho tam giác abc, vẽ tia đối blabala....
a) chứng minh tam giác này bằng tam giác kia
Vậy kết luận chính là câu a, còn giả thuyết là phần "cho tam giác...."
Nhưng chẳng có gì nói rằng kết luận đó đúng cả hay nói cách khác là người đọc nhìn thấy nhưng chưa tin
Thử lấy vd cho dễ hiểu: 1 thằng nói cái ghế trước mặt bạn đang dính nước, bạn không tin => nó phải chứng minh lời nói của nó đúng để bạn tin.
Vậy chứng minh là làm sao để người đọc hay thằng chấm bài hiểu rằng kết luận đúng.
Cách chứng minh: Giả thuyết người ta đưa không phải để nhìn cho vui, cả kiến thức môn hình trên trường cũng vậy. Phải biết kết hợp 2 cái lại để có thể chứng minh kết luận đúng.
Quay lại câu hỏi: Cm tam giác cân kiểu gì?
Bạn học lại tính chất tam giác cân rồi dùng nó áp dụng nhé
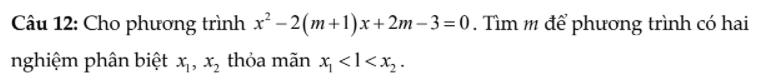
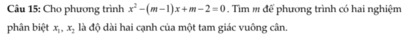
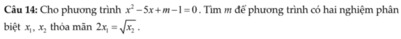
Không biết bạn biết cách làm dạng bài này chưa nhỉ? Nếu chưa mình sẽ bày dạng làm để áp dụng. Chứ nói thật làm xong mớ này bạn đọc cũng rất khó hiểu á.
Mình biết làm câu 1 và 3 rồi bạn làm câu 2 đc ko bạn ?