Chọn câu trả lời đúng:Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó?
A. Đồng quy
B. Tạo thành tam giác
C. Trùng nhau
D. Cùng song song với một mặt phẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Tham khảo:
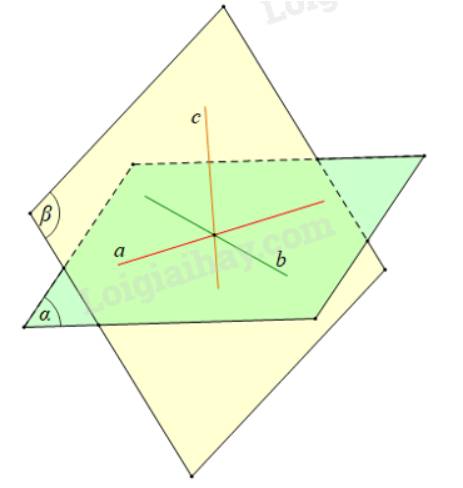
Giả sử a ∩ b = {I} và α = mp(a, b);
a ∩ c = {J} và β = mp(a, c);
b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.
Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.
α ∩ γ = b và đường thẳng b chính là đường thẳng IK.
β ∩ γ = c và đường thẳng c chính là đường thẳng JK.
Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)
Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.
Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.

Ta có: \(d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d\)
Lại có: \(M \in a\)
Mà qua \(M\) chỉ có một đường thẳng song song với đường thẳng \(b\) nên \(d \equiv a\).
Do đó \(a\parallel b\).

Gọi I = d1 ∩ d2; (P) là mặt phẳng chứa (d1) và (d2).
Gọi d3 ∩ d1 = M; d3 ∩ d2 = N.
+ M ∈ d1, mà d1 ⊂ (P) ⇒ M ∈ (P)
+ N ∈ d2, mà d2 ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ d3 có hai điểm M, N cùng thuộc (P)
⇒ d3 ⊂ (P)
⇒ d1; d2; d3 đồng phẳng (trái với giả thiết).
⇒ M ≡ N
⇒ M ≡ N ≡ I
Vậy d1; d2; d3 đồng quy.

Đáp án A
(1) Sai vì ( α ) // a ( β ) // a ( α ) ∩ ( β ) = d ⇒ a / / d tức là có trường hợp chúng cắt nhau.
Đáp án A