Cho phương trình z2 + mz - 6i = 0 Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + bi). Giá trị a + 2b là:
A. 0
B. 1
C.- 2
D. - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
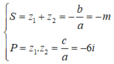
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
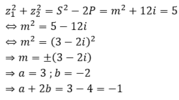

Chọn D
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
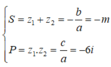
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
![]()
![]()
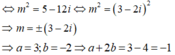

Chọn C.
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
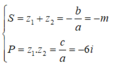
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
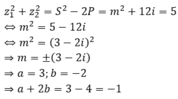

Chọn A.
Gọi z1, z2 là hai nghiệm của phương trình.
Theo Viet, ta có:
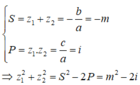
Để tổng bình phương hai nghiệm bằng – 4i thì:
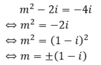

Chọn A.
Gọi z1; z2 là hai nghiệm của phương trình.
Theo Viet, ta có: 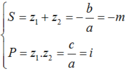
![]()
Ta có: m2 - 2i = - 4i khi và chỉ khi m2 = -2i hay m = ±( 1 - i)

Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung z 0 khi đó ta có hệ phương trình:
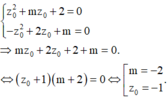
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: z 2 − 2 z + 2 = 0 trùng nhau nên có nghiệm chung.
TH2: Nếu z 0 = − 1 thay vào hệ ta được:
1 − m + 2 = 0 − 1 − 2 + m = 0 ⇔ m = 3 .
Vậy giá trị cần tìm là m = -2 và m = 3.

Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung z 0 khi đó ta có hệ phương trình:
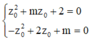
![]()
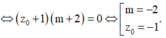
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: z 2 - 2z + 2 trùng nhau nên có nghiệm chung.
TH2: Nếu z 0 = -1 thay vào hệ ta được:

Vậy giá trị cần tìm là m = -2 và m = 3.

a) Thay \(x=0\) vào phương trình ta có:
\(\left(m-1\right).0^2-2m.0+m+1=0.\\ \Leftrightarrow m+1=0.\\ \Leftrightarrow m=-1.\)
b) Ta có: \(\Delta'=m^2-\left(m-1\right)\left(m+1\right).\)
\(\Delta'=m^2-\left(m^2-1\right).\\ =m^2-m^2+1.\\ =1>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
Theo Viet: \(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m+1}{m-1}.\\x_1+x_2=\dfrac{2m}{m-1}.\left(1\right)\end{matrix}\right.\)
Theo đề bài: \(x_1.x_2=5.\)
\(\Rightarrow\dfrac{m+1}{m-1}=5.\\ \Leftrightarrow m+1=5m-5.\\ \Leftrightarrow4m-6=0.\\ \Leftrightarrow m=\dfrac{3}{2}.\)
Thay \(m=\dfrac{3}{2}\) vào \(\left(1\right):\)
\(x_1+x_2=\) \(\dfrac{2.\dfrac{3}{2}}{\dfrac{3}{2}-1}=\dfrac{3}{\dfrac{1}{2}}=6.\)
Chọn D.
Gọi z1; z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
Suy ra: m2 = 5 - 12i
Do đó: m = ± ( 3 - 2i)
Vậy a = 3 ; b = -2 và a + 2b = -1