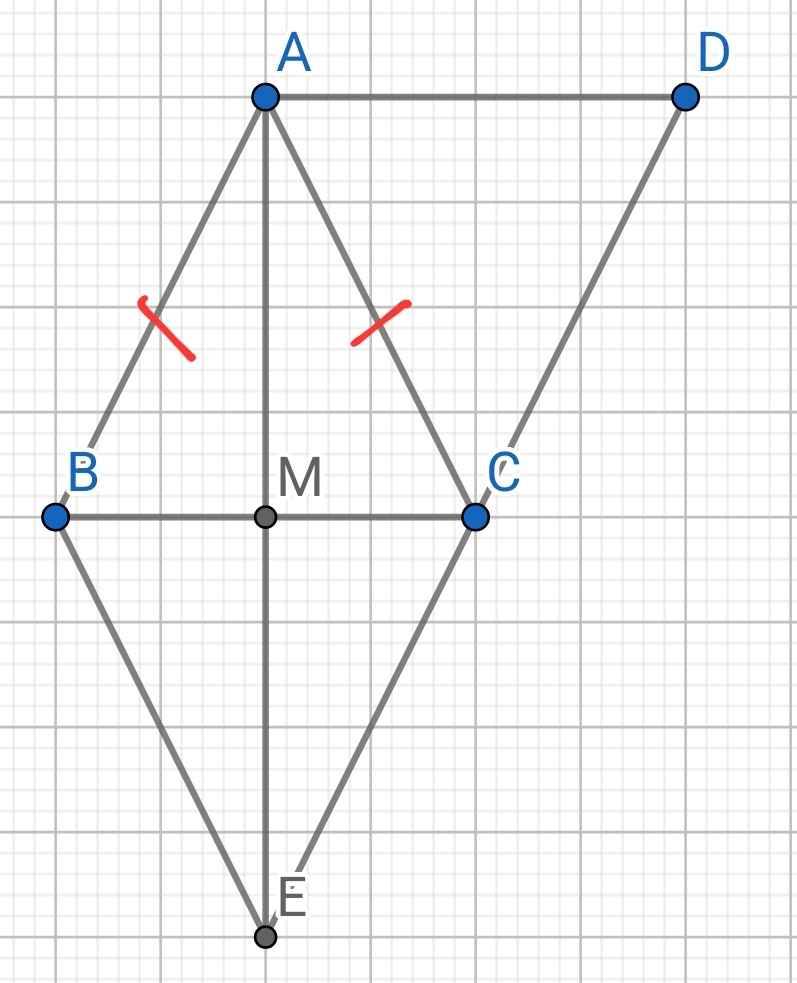
Cho hình bình hành ABCD có AB=AC. Qua B kẻ đường thẳng song song với AC cắt DC tại E
a, C/m tứ giác ABEC là hình thoi
b, C/m AE⊥BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2023
a: Xét tứ giác ABEC có
AB//EC
AC//BE
=>ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi
b: ABEC là hình thoi
=>AE vuông góc BC
KV
18 tháng 8 2023
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AB // CE
Tứ giác ABEC có:
AB // CE (cmt)
BE // AC (gt)
⇒ ABEC là hình bình hành
Mà AB = AC (gt)
⇒ ABEC là hình thoi
b) Do ABCD là hình thoi (cmt)
AE và BC là hai đường chéo của hình thoi
⇒ AE ⊥ BC
9 tháng 7 2022
a: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà góc B=góc C
nên BMNC là hình thang cân
b: Xét tứ giác BMEF có
BM//FE
ME//BF
Do đó: BMEF là hình bình hành
c: Xét ΔIFC và ΔIEN có
góc ICF=góc INE
IC=IN
góc CIF=góc NIE
Do đo; ΔIFC=ΔIEN
Suy ra: IE=IF
hay I là trung điểm của EF
Xét tứ giác NECF có
I là trung điểm của NC
I là trung điểm của EF
Do đó:NECF là hình bình hành
Suy ra: NE=CF
21 tháng 5 2022
a Xét tứ giác ABED có AB//ED
nên ABED là hình thang
b:
Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
Ta có: ABCD là hình thang cân
nên AC=BD
mà AC=BE
nên BD=BE
=>ΔBDE cân tại B
c: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
a: Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi