Trong các hàm số sau đâu là hàm hằng
A. y = x
B. y = 2x + 1
C. y = 2
D. y = 5/x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)

a: y=2x-1
a=2>0
=>Hàm số đồng biến
b: y=-3x+5
a=-3<0
=>Hàm số nghịch biến
c: \(y=\left(\sqrt{3}-\sqrt{2}\right)\cdot x\)
\(a=\sqrt{3}-\sqrt{2}>0\)
=>Hàm số đồng biến
d: \(y=-\dfrac{1}{2}\sqrt{x}+1\)
Vì -1/2<0 nên hàm số nghịch biến

Các hàm số là hàm số bậc nhất:
a) y = 3x - 2
b) y = -2x
d) y = 3(x - 1)

\(y=\dfrac{1}{2}\left(x^2-1\right)\) không phải hàm số bậc nhất

\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 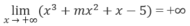
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

Hàm \(y = \cot x\)là hàm tuần hoàn với chu kì \(T = \pi \)do :
- Tập xác định là \(D = R\backslash \left\{ {k\pi ;k \in Z} \right\}\)
- Với mọi \(x \in D\), ta có \(x - \pi \; \in D\) và \(x + \pi \in D\;\)
Suy ra
\(\begin{array}{l}f\left( {x + \pi } \right) = \cot \left( {x + \pi } \right) = \cot \left( x \right) = f(x)\\f\left( {x - \pi } \right) = \cot \left( {x - \pi } \right) = \cot \left( x \right) = f\left( x \right)\end{array}\)

a: Đây là hàm số bậc nhất
a=2; b=-3
b: Đây là hàm số bậc nhất
a=-6; b=-7
c: Đây ko là hàm số bậc nhất
Đáp án C
Xét hàm số y =2. Với mọi giá trị của x nhưng y luôn nhận giá trị là 2 nên hàm số y =2 là hàm hằng.