Hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b'(a' ≠ 0) cắt nhau khi:
A. a ≠ a'
B. a ≠ a ' b ≠ b '
C. a = a ' b ≠ b '
D. a ≠ a ' b = b '
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
d cắt d' ⇔ a ≠ a'

Đáp án A
Cho hai đường thẳng d: y = ax + b(a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
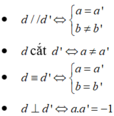

Đáp án A
Cho hai đường thẳng d: y = ax + b(a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
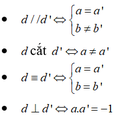

Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)
- Cắt nhau khi và chỉ khi a ≠ a'
- Song song với nhau khi và chỉ khi a = a', b ≠ b'
- Trùng nhau khi và chỉ khi a = a', b = b'

Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)
- Cắt nhau khi và chỉ khi a ≠ a'
- Song song với nhau khi và chỉ khi a = a', b ≠ b'
- Trùng nhau khi và chỉ khi a = a', b = b'

Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)
- Cắt nhau khi và chỉ khi a ≠ a'
- Song song với nhau khi và chỉ khi a = a', b ≠ b'
- Trùng nhau khi và chỉ khi a = a', b = b'
Đường thẳng song song Cho đường thẳng d có phương trình là y = a x + b ( a ≠ 0 ) y=ax+b(a≠0) và đường thẳng d' có phương trình là y = a ′ x + b ′ ( a ′ ≠ 0 ) y=a′x+b′(a′≠0). Khi đó d và d' song song khi và chỉ khi a = a ′ a=a′ và b ≠ b ′ b≠b′ Chú ý: nếu a=a' và b=b' thì d trùng d' 2. Đường thẳng cắt nhau Cho đường thẳng d có phương trình là y = a x + b ( a ≠ 0 ) y=ax+b(a≠0) và đường thẳng d' có phương trình là y = a ′ x + b ′ ( a ′ ≠ 0 ) y=a′x+b′(a′≠0). Khi đó d và d' cắt nhau khi và chỉ khi a ≠ a ′ a≠a′ Chú ý: nếu a ≠ a ′ a≠a′ và b=b' thì d cắt d' tại một điểm trên trục tung có tung độ là b

Phương trình tổng quát của đường thẳng \(d,d'\) lần lượt là: \(ax - y + b = 0,{\rm{ }}a'x - y + b' = 0\).
Do đó \(\overrightarrow {{n_d}} = \left( {a; - 1} \right),{\rm{ }}\overrightarrow {{n_{d'}}} = \left( {a'; - 1} \right)\).
Ta có \(d \bot d' \Leftrightarrow \overrightarrow {{n_d}} \bot \overrightarrow {{n_{d'}}} \Leftrightarrow \overrightarrow {{n_d}} .\overrightarrow {{n_{d'}}} = 0 \Leftrightarrow a.a' + \left( { - 1} \right)\left( { - 1} \right) = 0 \Leftrightarrow a.a' = - 1\).

- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi chúng không có điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi chúng có một điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau khi chúng có vô số điểm chung.
Đáp án A
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
d cắt d' ⇔ a ≠ a'