Cho tứ diện ABCD có CD = 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính cotan của góc giữa hai mặt phẳng (ACD) và (BCD)?
A. 3 4
B. 3 5
C. 5 3
D. 4 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
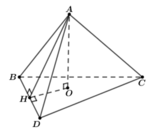
Gọi O là chân đường vuông góc kẻ từ A đến mặt phẳng (BCD)
![]()
![]()
![]()
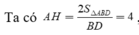
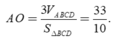
Khi đó ta tính được
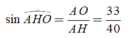

Đáp án C
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0

Chọn C
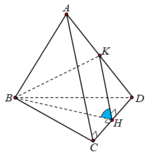
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
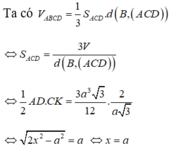
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
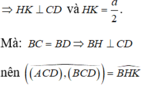
Mặt khác:
Tam giác ABD có:
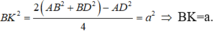
Tam giác BHK có:
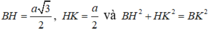
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o

Chọn A
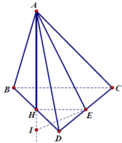
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3
Đáp án D
Gọi H là hình chiếu của A trên (BCD) ⇒ A H ⊥ B C D
Ta có V A B C D = 1 3 A H . S ∆ B C D ⇒ A H = 3 V S ∆ B C D = 3 . 20 10 = 6
Và S ∆ A C D = 1 2 A K . C D ⇒ A K = 2 . S C D = 2 . 15 3 = 10
Tam giác AHK vuông tại H, có c o t A K H ^ = H K A H = 10 2 - 6 2 6 = 4 3