Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có vecto pháp tuyến là n → = (2; –1;1). Vectơ nào sau đây cũng là vectơ pháp tuyến của (P)?
A. (–2;1;1)
B. (–4;2;3)
C. (4;2; –2)
D. (4; –2;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 1 2018
Đáp án A
( 4 ; − 2 ; 2 ) = 2 ( 2 ; − 1 ; 1 ) ⇒ ( 4 ; − 2 ; 2 ) là một VTPT của (P)
CM
24 tháng 8 2019
Đáp án D
Phương pháp : Nếu n → là 1VTPT của (P) ⇒ k n → ( k ≠ 0 ) cũng là 1 VTPT của (P)
CM
14 tháng 8 2019
Đáp án D.
Mặt phẳng (P) có vecto pháp tuyến (VTPT) là n P → = 3 ; 2 ; − 1
Ghi nhớ: Mặt phẳng P : a x + b y + c z + d = 0 có VTPT là n → = a ; b ; c , với a 2 + b 2 + c 2 ≠ 0
CM
19 tháng 10 2017
Đáp án C.
Phương pháp:
Mặt phẳng P : A x + B y + C z + D = 0 có 1 VTPT là n → = A ; B ; C .
Cách giải:
P : x − 4 y + 3 z − 2 = 0 có một vecto pháp tuyến là n 3 → = − 1 ; 4 ; − 3 .
CM
5 tháng 5 2019
Đáp án D
Phương trình mặt phẳng (P) đi qua điểm M và có vectơ pháp tuyến n → là:
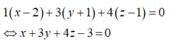
Đáp án D
Phương pháp : Nếu n → là 1VTPT của (P) => k n → (k≠0) cũng là 1 VTPT của (P)