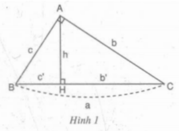
Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
7 tháng 1 2019
Xét tam giác ABC vuông tại A có
SABC = 1/2 AB.AC
Xét tam giác ABC có AH là đường cao
⇒ SABC = 1/2 AH.BC
⇒ 1/2 AB.AC = 1/2 AH.BC ⇒ AB.AC = AH.BC hay bc = ah
20 tháng 5 2022
2:Trọng tâm(điểm này được gọi là G)
3:Tham khảo:https://giaibaitap123.com/giai-toan-lop-7-tap-2/bai-9-nghiem-cua-da-thuc-mot-bien/
5:Đối với tam giác thường:
CC
CGC
GCG
Đối với tam giac vuông là:
CHGN
6:Tham khảo:
https://hanghieugiatot.com/cach-chung-minh-duong-trung-truc-lop-7
20 tháng 5 2022
Câu 1: Để xác định bậc của một đa thứ , bạn cần làm là tìm số mũ lớn nhất trong đa thức đó
Câu 2: Giao của 3 đường trung tuyến được gọi là trọng tâm
Câu 3: Nghiệm của đa thức là a nếu tại x=a đa thứ P(x) có giá thị bằng 0=> để tìm nghiệm của đa thức 1 biến, hãy cho đa thức đó bằng 0 và giải như cách giải phương trình 1 ẩn
Câu 4: Hai đa thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phân biến. Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến. Các số khác 0 được gọi là những đơn thức đồng dạng
Câu 5:
* Đối với tam giác thường
+ Trường hợp cạnh-cạnh-cạnh
+Trường hợp cạnh-góc-cạnh
+Trường hợp góc-cạnh-góc
*Đối với tam giác vuông
+ Trường hợp cạnh góc vuông-cạnh góc vuông
+Trường họp cạnh góc vuông- góc nhọn
+ Trường hợp cạnh huyền-góc nhọn
Câu 6:
Phương pháp 1: Chúng ta phải phải chứng minh rằng d\(\perp\)AB tại ngay trung điểm của AB
Phương pháp 2: Chứng minh rằng 2 điểm trên d cách đề 2 điểm A và B
Phương pháp 3: Dùng tính chất đường trung tuyến , đường cao
Phương pháp 4: Áp dụng tính chất đối xúng của trục
Phương pháp 5: Áp dụng tính chất nối tâm của 2 đường tròn cắt nhau ở 2 điểm
14 tháng 4 2023
a: Xét ΔBEC và ΔAEFcó
góc BEC=góc AEF
góc ECB=góc EFA
=>ΔBEC đồng dạng với ΔAEF
b: Xét ΔFEA và ΔFCD có
góc FEA=góc FCD
góc F chung
=>ΔFEA đồng dạng với ΔFCD
10 tháng 5 2023
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP
8 tháng 7 2023
Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
Xét tam giác ABC vuông tại A có
SABC = 1/2 AB.AC
Xét tam giác ABC có AH là đường cao
⇒ SABC = 1/2 AH.BC
⇒ 1/2 AB.AC = 1/2 AH.BC ⇒ AB.AC = AH.BC hay bc = ah