Cho tam giác ABC cân tại A, đường cao BE cắt đường trung tuyến AD ở H. Chứng minh C H ⊥ A B .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

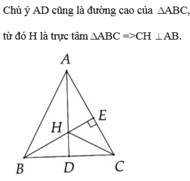

a: Xét ΔABC có
AD,BE là đường cao
AD cắt EB tại H
=>H là trực tâm
=>CH vuông góc AB
b: ΔABC cân tại A
mà AD là trung tuyến
nên AD vuông góc BC
Xét tứ giác AKBD có
góc AKB=góc ADB=góc KBD=90 độ
=>AKBD là hình chữ nhật
=>góc KAD=90 độ

a: Xét ΔABC có
AD,BE là đường cao
AD cắt EB tại H
=>H là trực tâm
=>CH vuông góc AB
b: ΔABC cân tại A
mà AD là trung tuyến
nên AD vuông góc BC
Xét tứ giác AKBD có
góc AKB=góc ADB=góc KBD=90 độ
=>AKBD là hình chữ nhật
=>góc KAD=90 độ

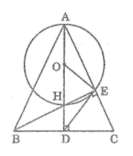
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
![]()
Trong tam giác BDH ta có:
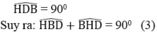
Từ (1), (2) và (3) suy ra:
![]()
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
![]()
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).

Bài 2)
b) Do DE=BD nên tam giác BDE cân tại D nên ^DEB=^DBE
Tam giác OEH cân tại O nên ^OEH=^OHE=^BHD (đối đỉnh)
Do đó ^DEB+OEH=^DBE+BHD=90*
suy ra OE vuông góc với DE
nên DE là tiếp tuyến của (O)
câu c) Xét tam giác vuông OED có OE=AH/2=3cm, OD=OH+HD=5cm
nên theo Pitago thì DE^2=OD^2-OE^2=5^2-3^2=4^2 suy ra DE = 4cm
nhớ k mình nhé cảm ơn nhiều

ΔABC cân tại A
mà AD là trung tuyến
nên AD là đường cao
Xét ΔABC có
AD,BE,CF là các đường cao
BE cắt CF tại H
=>A,H,D thẳng hàng