Tìm x, y thoả mãn: 3 x − 4 + 3 y + 5 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

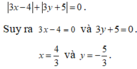


\(\left(\dfrac{3x-5}{9}\right)^{2018}>=0\forall x\)
\(\left(\dfrac{3y+0,4}{3}\right)^{2020}>=0\forall y\)
Do đó: \(\left(\dfrac{3x-5}{9}\right)^{2018}+\left(\dfrac{3y+0,4}{3}\right)^{2020}>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}\dfrac{3x-5}{9}=0\\\dfrac{3y+0,4}{3}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-5=0\\3y+0,4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=-\dfrac{0.4}{3}=-\dfrac{2}{15}\end{matrix}\right.\)


\(y=\dfrac{1}{3}\left(m-1\right)x^3-\left(m-1\right)x^2+\left(m+3\right)x-2\)
\(y'=\)\(x^2\left(m-1\right)-2x\left(m-1\right)+m+3\)
a)\(y'=0\)\(\Leftrightarrow x^2\left(m-1\right)-2x\left(m-1\right)+m+3=0\)
Xét m=1 => pt tt: 3=0 (vô lí)
=> \(m\ne1\)
Để y'=0 có hai nghiệm pb cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-16m+16>0\\\dfrac{m+3}{m-1}>0\end{matrix}\right.\)\(\Rightarrow m< -3\)
b)y'=0 có hai nghiệm \(\Leftrightarrow\Delta\ge0\) \(\Leftrightarrow m\le-3\)
Theo viet có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m-1}=2\\x_1x_2=\dfrac{m+3}{m-1}\end{matrix}\right.\)
Có x12+x22=4
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\)\(4-\dfrac{2\left(m+3\right)}{m-1}=4\)
\(\Leftrightarrow m=-3\) (tm)
Vậy m=-3
(đúng không ạ?)