Một lò xo có độ cứng k, bị kéo giãn ra một đoạn x. Thế năng đàn hồi của lò xo được tính bằng biểu thức
A. W t = 1 2 k x 2
B. W t = 1 2 k 2 x
C. W t = 1 2 k x
D. W t = 1 2 k 2 x 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tần số góc của dao động ω = k m = 100 0 , 2 = 10 5 rad/s → T = 0,281 s.
+ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 2 cm
→ Kéo vật xuống vị trí lò xo giãn 6 cm rồi thả nhẹ → lò xo sẽ dao động với biên độ A = 6 – 2 = 4 cm.
+ Với E d = E d h ↔ E – E t = E d h → 1 2 k A 2 − 1 2 k x 2 = 1 2 k Δ l 0 + x 2 → 2 x 2 + 2 Δ l 0 x + Δ l 0 2 − A 2 = 0
Thay các giá trị đã biết vào phương trình, ta thu được x 2 + 2 x – 6 = 0 → hoặc x = 1,65 cm hoặc x = –3,65 cm.
→ Thời gian gần nhất kể từ thời điểm ban đầu (vật đang ở biên là) Δ t min = a r cos 1 , 65 4 360 0 0 , 281 = 51 , 3 m s

Đáp án A.
Khi lò xo bị nén lại một đoạn Δl thì thế năng đàn hồi bằng 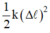

Lời giải
Công thức tính thế năng đàn hồi của lò xo:
W t = 1 2 k Δ l 2 trong đó Δl: độ biến dạng của lò xo
Đáp án: A

Chọn đáp án A
Thế năng đàn hồi của lò xo là: W t = 1 2 k ∆ l 2
Lời giải
Công thức tính thế năng đàn hồi của lò xo:
W t = 1 2 k Δ l 2 trong đó Δl: độ biến dạng của lò xo
Đáp án: A