Cho tứ diện ABCD và 3 điểm E, F, G lần lượt nằm trên 3 cạnh AB, BC, CD mà không trùng với các đỉnh, thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:
A. một đoạn thẳng
B. một tam giác
C. một tứ giác
D. một hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Trong mặt phẳng (BCD), F G ∩ B D = H
H ∈ BD ⇒ H ∈ (ABD)
Trong (ABD), E H ∩ A D = I
⇒ tứ giác EFGI là thiết diện cần tìm

Đáp án B
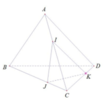
Thiết diện của hình chóp khi cắt bởi mp (IJK) là tam giác IJK.

Đáp án A
Hiển nhiên thiết diện của hình tứ diện A B C D khi cắt bởi mặt phẳng M N P là một tam giác

Đáp án A
Hiển nhiên thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là một tam giác.

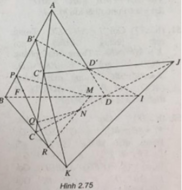
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt

Đáp án D
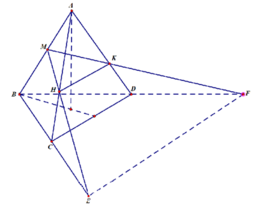
Thiết diện cần tìm là MHK
Ta có:
H là trọng tâm tam giác ABE
K là trọng tâm tam giác ABF
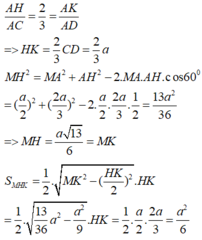

Đáp án D
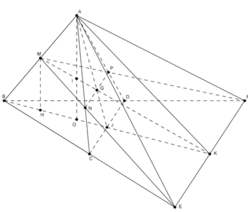

Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
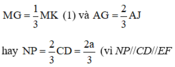
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là


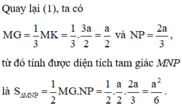
Đáp án C
Trong (ABC) có EF ∩ AC = I
⇒ I ∈ (ACD)
Xét (ACD) có: IG ∩ AD = H
⇒ EFGH là thiết diện cần tìm