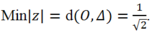Cho số phức z thỏa mãn |z +1 +i | =| z ¯ - 2i |. Tìm giá trị nhỏ nhất của |z|.
A. 2
B. 1
C. 1 2
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho số phức z thỏa mãn |z +1 +i | =| z ¯ - 2i |. Tìm giá trị nhỏ nhất của |z|.
A. 2
B. 1
C. 1 2
D. 2


Chọn B.
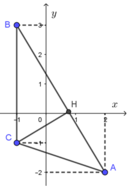
Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)
Phương trình đường thẳng AB: 5x + 3y - 4 = 0.
Khi đó theo đề bài ![]()
Ta có ![]() . Do đó quỹ tích M là đoạn thẳng AB.
. Do đó quỹ tích M là đoạn thẳng AB.
Tính CB = 4 và ![]() .
.
Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
Vậy 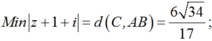
![]()

Đáp án C
Đặt z = x + y i x , y ∈ ℝ ,
khi đó
z − 3 − 2 i ≤ 1 ⇔ x − 3 2 + y − 2 2 ≤ 1
Suy ra tập hợp điểm biểu diễn số phức z là miền trong đường tròn
x − 3 2 + y − 2 2 = 1.
Đặt w = a + b i a , b ∈ ℝ , khi đó w + 1 + 2 i ≤ w − 2 − i ⇔ a + b ≤ 0
Suy ra tập hợp điểm biểu diễn số phức w là miền x + y ≤ 0 , bờ là đường thẳng x + y = 0 .
Gọi C : x − 3 2 + y − 2 2 = 1 có tâm I 3 ; 2 , bán kính R = 1 và Δ : x + y = 0 .
Do đó
P = z − w = M N ⇒ M N min = d I ; Δ − R = 5 2 − 1 = 5 2 − 2 2 .

Chọn đáp án A
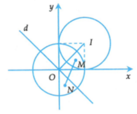

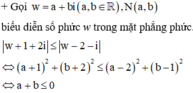
=> Tập hợp các điểm M là nửa mặt phẳng không chứa điểm I(1;1), có bờ là đường thẳng x + y = 0 (d)


Đáp án B
Gọi: ![]()
Ta có:
![]()
![]()
![]()
![]()
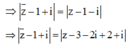
![]()
![]()
=> Giá trị nhỏ nhất của z ¯ -1-i| là 5 - 1
Chọn C.
Gọi z = x+ yi thì M (x; y) là điểm biểu diễn z
Ta có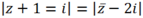
Nên ( x + 1) 2 + (y + 1) 2 = x2 + (y + 2) 2 hay ∆: x – y – 1 = 0.
Do đó điểm M di chuyển trên ∆. Do đó; để modul của số phức z min khi M là hình chiếu của O trên ∆
Vậy