Cho tam giác ABC vuông cân tại A.Trên cạnh BC lấy các điểm H,G sao cho BG theo thứ tự ở E và F.Tứ giác EFGH là hình gì?Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


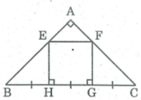
Vì ΔABC vuông cân tại A nên ∠ B = ∠ C = 45 0
Vì ΔBHE vuông tại H có ∠ B = 45 0 nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có ∠ C = 45 0 nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có ∠ (EHG) = 90 0 nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.

Tam giác vuông FGC có \(\widehat{C}=45^0\) nên là tam giác vuông cân. Do đó FG = GC


đó là hình bình hành đó bạn ơi.
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)
Chúc bạn thành công...
tk nha bạn
thank you bạn
a, Ta noi AC lai voi nhau .
Xet tam giac ABD co :
AH=HD a AE=EB
=> HE la dtb => HE=1/2BD va HE//DB (1)
Xet tam giac BDC co :
DG=GC va BF=FC
=> GF la dtb => GF=1/2BD va GF//BD (2)
Tu (1) va (2) suy ra : HE//GF va HE=GF
Hay tứ giác EFGH la HBH
b, Nếu AC vuông góc với BD thì tứ giác EFGH là hình HCN vì :
Ta có : AC//EF va BD//HE
=> E=90
Hay hình bình hành EFGH là hình chữ nhật ( hình bình hành có 1 góc vuông là hình chữ nhật)
c, Áp dụng định lý pi-ta-go là :
AO2+OB2=AB2
x2+82=102
x2=102-82
x2=36
=>x=6
Dien h tam giac AOB la :
\(\frac{1}{2}.6.8=24cm^2\)
Vay dien h tam giac AOB la 24cm2
Câu a bạn có thể kham khảo bài của bạn le anh tu (co 2 cach)
nho k nha

Bài 2:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

Xét tam giác ABC có: EB=EA (gt); BF=FC (gt)
EF là đường trung bình của tam giác ABC
EF//AC; EF=1/2AC (1)
Xét tam giác ADC có: AH=HD (gt); CG=DG (gt)
HG là dường trung bình của tam giác ADC
HG//AC; HG=1/2AC (2)
Từ (1) và (2) EF//HG; EF=HG
EFGH là hình bình hành
Ta có EH là đường trung bình của tam giác ABD
vì AE=EB; AH=HD
EH//BD
mà AC BD; EH=BD; EF//AC
EFEH hay E=
Vậy EFGH là hình chữ nhật.

1:
ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
EH\(\perp\)BC tại H
=>EH\(\perp\)HB tại H
=>ΔEHB vuông tại H
Xét ΔHEB vuông tại H có \(\widehat{HBE}=45^0\)
nên ΔHEB vuông cân tại H
FG\(\perp\)BC tại G
=>FG\(\perp\)GC tại G
=>ΔFGC vuông tại G
Xét ΔFCG vuông tại G có \(\widehat{GCF}=45^0\)
nên ΔFCG vuông cân tại G
2: EH\(\perp\)BC
FG\(\perp\)BC
Do đó: EH//FG
EH=HB
HB=HG=GC
GF=GC
Do đó; EH=HB=GH=CG=GF
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHFG là hình bình hành
Hình bình hành EHFG có \(\widehat{EHG}=90^0\)
nên EHFG là hình chữ nhật
Hình chữ nhật EHFG có GH=GF
nên EHFG là hình vuông
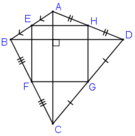
Đề thiếu rồi bạn