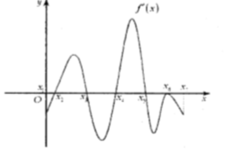
Cho hàm số có đồ thị như hình bên. Biết rằng: và Giá trị lớn nhất của hàm số trên bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

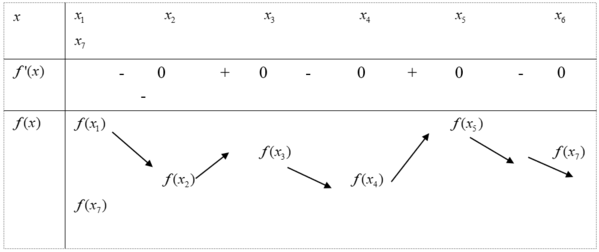


Xét 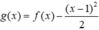 có
có
![]()
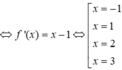
Vì đường thẳng y=x-1 cắt đồ thị f '(x) tại 4 điểm có hoành độ x=-1, x=1, x=2, x=3
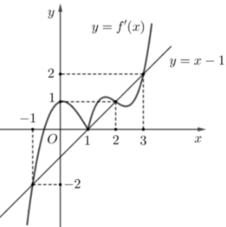

Suy ra g(x) có ba điểm cực trị là x=-1, x=1, x=2, x=3
Theo giả thiết  có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
Chọn đáp án B.
*Chú ý số điểm cực trị của hàm số y=|g(x)| bằng tổng số điểm cực trị của f(x) và số nghiệm đơn (hoặc bội lẻ) của phương trình f(x)=0
Chọn đáp án B.

Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.

Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến

Dựa vào đồ thị hàm số f'(x) suy ra đồ thị hàm số đồng biến trên khoảng (-3;-2), đồ thị hàm số nghịch biến trên khoảng ![]()
Chọn B.

Đáp án D.
- Để vẽ đồ thị hàm số y = |f(x)| ta lấy đối xứng phần đồ thị hàm số nằm phía dưới trục hoành lên phía trên.
- Đồ thị hàm số y = |f(x)| có 3 điểm cực trị như hình vẽ: