cho đường tròn tâm 0 , điểm M cố định nằm ngoài đường tròn , từ M vẽ cát tuyến qua đường tròn , cắt đường tròn tại E và F , Chứng minh ME . MF không đổi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BB
Ba Ba
15 tháng 1 2016
Đúng(0)
Những câu hỏi liên quan
17 tháng 5 2021
a) Xét (O) có
\(\widehat{EFA}\) là góc nội tiếp chắn cung EA
\(\widehat{EBA}\) là góc nội tiếp chắn cung EA
Do đó: \(\widehat{EFA}=\widehat{EBA}\)(Hệ quả góc nội tiếp)
hay \(\widehat{MBE}=\widehat{MFA}\)
Xét ΔMBE và ΔMFA có
\(\widehat{MBE}=\widehat{MFA}\)(cmt)
\(\widehat{AMF}\) chung
Do đó: ΔMBE∼ΔMFA(g-g)
Suy ra: \(\dfrac{MB}{MF}=\dfrac{ME}{MA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=ME\cdot MF\)(Đpcm)
3 tháng 12 2023
a:Xét (O) có
MF,ME là tiếp tuyến
Do đó: MF=ME
=>M nằm trên đường trung trực của FE(1)
OE=OF
=>O nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra OM là đường trung trực của EF
=>OM\(\perp\)EF tại H và H là trung điểm của EF
b: ΔOMF vuông tại F
=>\(FO^2+FM^2=OM^2\)
=>\(FM^2=10^2-6^2=64\)
=>\(FM=\sqrt{64}=8\left(cm\right)\)
Xét ΔOFM vuông tại F có FH là đường cao
nên \(OH\cdot OM=OF^2\)
\(\Leftrightarrow OH\cdot10=6^2=36\)
=>OH=36/10=3,6(cm)
c: Xét tứ giác BHMA có
\(\widehat{BHM}+\widehat{BAM}=90^0+90^0=180^0\)
=>BHMA là tứ giác nội tiếp
=>B,H,M,A cùng thuộc một đường tròn
CM
26 tháng 7 2018
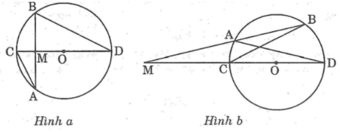
*Trường hợp M nằm bên trong đường tròn (O) (hình a)
Kẻ cát tuyến AB đi qua M và đường thẳng MO cắt đường trong tại C và D
Xét hai tam giác MBD và MCA ta có:
Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (*) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
*Trường hợp M nằm bên ngoài đường tròn (O) (hình b)
Kẻ cát tuyến MAB bất kì của (O) và đường thẳng MO cắt đường tròn tại C và D
Xét hai tam giác MCB và MAD ta có:
Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (**) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
9 tháng 2 2020
a, Xét tứ giác MEOF có \(\widehat{MEO}=\widehat{MFO}=90^0\)
=> Tứ giác MEOF nội tiếp (t/c)
=> 4 điểm M,E,O,F cùng thuộc đường tròn đường kính MO (1)
Xét tứ giác AFOM có : \(\widehat{MAO}=\widehat{MFO}=90^0\)
=> Tứ giác AFOM nội tiếp (t/c)
=> 4 điểm M,A,O,F cùng thuộc đường tròn đường kính MO (2)
Từ (1) và (2) => Năm điểm A, M, E, O, F cùng thuộc đường tròn đường kính MO
