Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A với A B = A C = a , cạnh S A = S B = a và có S B C ⊥ A B C . Tính SC để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng a.
A. S C = a
B. S C = a 2
C. S C = a 3
D. S C = 2 a .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì 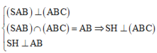
Tam giác SAB vuông cân tại S nên SA = SB = a 2
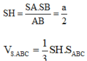
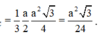

Đáp án C
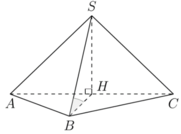
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12

Đáp án D.
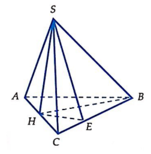
Đặt SH = x, tính SB, SC theo x. Sau đó áp dụng định lí cosin cho ∆ SBC
Tìm được ![]()

Đáp án A
Gọi H là trung điểm của AB suy ra S H ⊥ A B
Do Δ S A B vuông cân tại S nên S H = A B 2 = a 2 ; S A B C = a 2 2 ⇒ V = a 3 12 .
Đáp án C
Gọi H là trung điểm B C ⇒ A H ⊥ B C ⇒ A H ⊥ S H
Ta có Δ S H A = Δ B H A , Δ S B C vuông tại S ⇒ R b = B H = B C 2
R = R b 2 + R d 2 − B C 2 4 = a
Xét Δ A B C có
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = a 3
Ta có trong tam giác vuông S B C : S C = B C 2 − S B 2 = a 2