Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=\dfrac{x^{\dfrac{1}{3}}\cdot y^{\dfrac{1}{2}}+y^{\dfrac{1}{3}}\cdot x^{\dfrac{1}{2}}}{x^{\dfrac{1}{6}}+y^{\dfrac{1}{6}}}=\dfrac{x^{\dfrac{1}{3}}\cdot y^{\dfrac{1}{3}}\left(x^{\dfrac{1}{6}}+y^{\dfrac{1}{6}}\right)}{x^{\dfrac{1}{6}}+y^{\dfrac{1}{6}}}=x^{\dfrac{1}{3}}\cdot y^{\dfrac{1}{3}}=\left(xy\right)^{\dfrac{1}{3}}\)
b: \(B=\dfrac{x^{3+\sqrt{3}}}{y^2}\cdot\dfrac{x^{-\sqrt{3}-1}}{y^{-2}}=\dfrac{x^{3+\sqrt{3}-\sqrt{3}-1}}{y^{2-2}}=x^2\)

Đáp án B.
Ta có A = a 1 3 b + b 1 3 a a 6 + b 6 = a 1 3 b 1 3 b 6 + a 6 a 6 + b 6 = a 1 3 b 1 3 = a b 3 .

Đáp án B
Sử dụng máy tính tính giá trị của A với a=2;b=3 rồi lưu vào biến X:


Với A:


Kết quả ra khác 0 nên ta loại A.
Với B:
![]()

Vậy ta chọn B.

a: ta có: \(M=\dfrac{a}{\sqrt{ab}+b}+\dfrac{b}{\sqrt{ab}-a}-\dfrac{a+b}{\sqrt{ab}}\)
\(=\dfrac{a\left(\sqrt{ab}-a\right)+b\left(\sqrt{ab}+b\right)}{\left(\sqrt{ab}+b\right)\left(\sqrt{ab}-a\right)}-\dfrac{a+b}{\sqrt{ab}}\)
\(=\dfrac{-\sqrt{ab}\left(a+b\right)+\left(a-b\right)\left(a+b\right)}{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)\cdot\sqrt{a}\cdot\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{a+b}{\sqrt{ab}}\)
\(=\dfrac{-\sqrt{ab}\left(a+b\right)+\left(a-b\right)\left(a+b\right)}{\sqrt{ab}\left(a-b\right)}-\dfrac{a^2-b^2}{\sqrt{ab}\left(a-b\right)}\)
\(=\dfrac{-\sqrt{ab}}{\sqrt{ab}\left(a-b\right)}\)
\(=-\dfrac{1}{a-b}\)
b: Thay \(a=\sqrt{5}+1\) và \(b=\sqrt{5}-1\) vào M, ta được:
\(M=\dfrac{-1}{\sqrt{5}+1-\sqrt{5}+1}=\dfrac{-1}{2}\)

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
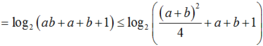
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Đáp án B