Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thể tích khối chứa điểm A’ và
V
2
là thể tích khối chứa điểm C’. Khi đó
V
1
V
2
là A.
25
47
.
B.1 C.
17
25
.
D.
...
Đọc tiếp
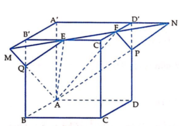
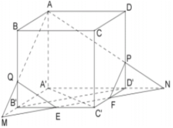
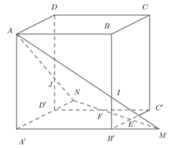
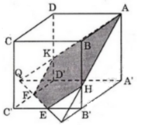
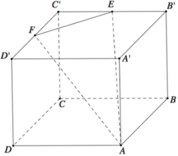
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là
A. 25 47 .
B.1
C. 17 25 .
D. 8 17 .
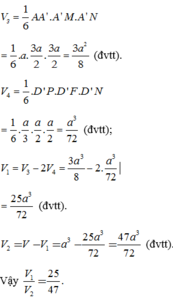
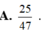
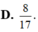
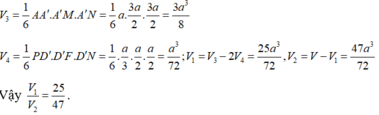
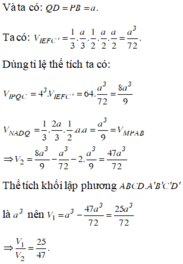
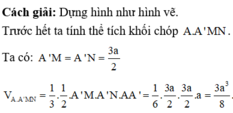
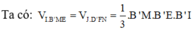
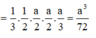
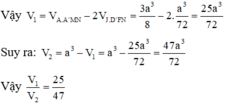
Đáp án A.
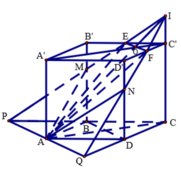
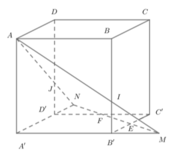
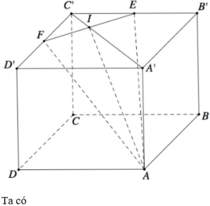
Đường thẳng EF cắt A'D' và A'B' tại N;M;AN cắt DD' tại P;AM cắt BB' tại Q. Khi đó thiết diện của hình lập phương khi cắt bởi mặt phẳng (AEF) là ngũ giác APFEQ
Từ giả thiết ta có V 1 = V A ' B ' D ' A P F E Q và V 2 = V A B C D C ' P F E Q ' .
Gọi
V = V A B C D . A ' B ' C ' D ' ; V 3 = V A . A ' M N ; V 4 = V P F D ' N ; V 5 = V Q M B ' E .
Do tính đối xứng của hình lập phương nên V 4 = V 5 .
Nhận thấy
V 3 = 1 6 A A ' . A ' M . A ' N = 1 6 . a . 3 a 2 . 3 a 2 = 3 a 2 8 (đvtt).
V 4 = 1 6 . D ' P . D ' F . D ' N = 1 6 . a 3 . a 2 . a 2 = a 3 72 (đvtt);
V 1 = V 3 − 2 V 4 = 3 a 3 8 − 2. a 3 72 = 25 a 3 72 (đvtt).
V 2 = V − V 1 = a 3 − 25 a 3 72 = 47 a 3 72 (đvtt).
Vậy V 1 V 2 = 25 47 .