Cho hàm số y = x 4 − 2 m x 2 + 2 m . Xác định tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị và các điểm cực trị này lập thành một tam giác có diện tích bằng 32.
A. m = 4, m = 1
B. m = 4
C. m = -4
D. m = -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có y ' = 4 x 3 − 4 m x = 4 x x 2 − m
Đồ thị hàm số có 3 điểm cực trị ⇔ y ' = 0 có ba nghiệm phân biệt, suy ra m > 0
Khi đó tọa độ ba điểm cực trị là A 0 ; 2 m , B m ; 2 m − m 2 , C − m ; 2 m − m 2
Suy ra H 0 ; 2 m − m 2 là trung điểm BC
⇒
A
H
=
m
2
B
C
=
2
m
⇒
S
A
B
C
=
1
2
A
H
.
B
C
=
1
2
m
2
.2
m
=
32
⇒
m
=
4

Đáp án D
Ta có y’ = 4mx3 – 2(m – 1)x.
y' = 0 ó 4mx3 – 2(m – 1)x = 0 ó
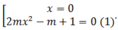
Để hàm số có 3 điểm cực trị
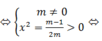
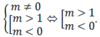

Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
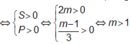
Vậy các giá trị cần tìm của m là m >1

Đáp án A.
Ta có g x = f x + m ⇒ g ' x = f ' x . f x + m f x + m . (Chú ý: u = u ' . u u ).
Để hàm số y = g(x) có 3 điểm cực trị ⇔ g ' x = 0 có 3 nghiệm phân biệt (1).
Mặt khác, phương trình g ' x ⇔ [ f ' x = 0 f x + m = 0 ⇔ [ x = x 1 ; x = x 2 f x = - m (2).
Từ (1), (2) suy ra [ - m ≥ 1 - m ≤ - 3 ⇔ [ m ≤ - 1 m ≥ 3 .

Đáp án D
Dựa vào đồ thị hàm số, dễ thấy hàm số f x = x 3 + 3 x 2 − 1
Xét hàm số f x + m = x + m 3 + 3 x + m − 1 với x ∈ ℝ
Chú ý : Cực trị là điểm làm y' đổi dấu và f x = x = x 2 ⇒ f ' x = 2 x 2 x 2 = x x
Do đó f x + m = 3 x + m x + m + 2 . x x .
Khi đó y = f x + m có 5 điểm cực trị x + m = 0 x + m + 2 = 0 có 4 nghiệm phân biệt x = − m x = − 2 − m có 4 nghiệm − m > 0 − 2 − m > 0 ⇔ m < − 2
Cách 2: Đồ thị hàm số y = f x + m được suy ra từ
y = f x → y = f x + m → y = f x + m .
Đồ thị hàm số muốn có 5 điểm cực trị khi ở bước thứ 1ta dịch chuyển đồ thị sang phải nhiều hơn 2 đơn vị m < − 2
Đáp án B
y ' = 4 x 3 − 4 m x = 4 x ( x 2 − m ) y ' = 0 ⇔ x = 0 x = ± m ⇒ A ( 0 ; 2 m ) , B ( m ; − m 2 + 2 m ) , C ( − m ; − m 2 + 2 m ) ⇒ S = 1 2 . 2 m + m 2 − 2 m .2 m = m 2 m = 32 ⇒ m = 4