Cho hình chóp S.ABC có SA = SB = SC = a 2 và đáy là tam giác ABC cân tại A. Biết BAC = 120 ° và BC = 2a. Thể tích khối chóp S.ABC là
A. a 3 2 6 .
B. a 3 3 9 .
C. a 3 2 9 .
D. a 3 2 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.


Đáp án D
Gọi H là trung điểm của BC.
Do tam giác ABC vuông cân tại A nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Mặt khác do SA=SB=SC nên S thuộc trục đường tròn ngoại tiếp ABC
⇒ S H ⊥ A B C A H = B C 2 = a , S H = S A 2 - A H 2 = a A B = A C = B C 2 a 2
Thể tích khối chóp là
V = 1 3 . S H . 1 2 . A B . A C = a 3 3

Đáp án B
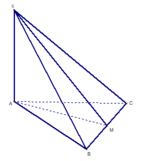
Gọi M là trung điểm của BC . Vì Δ A B C cân tại A nên A M ⊥ B C ,
Ta có A M ⊥ B C S M ⊥ B C S B C ∩ A B C = B C ⇒ Góc giữa S B C và A B C là góc Vì góc S A M = 90 0
Có B M = a , góc B A M = 60 0 nên
sin B A M = B M A B ⇒ A B = 2 a 3 ⇒ S Δ A B C = 1 2 A B . A C . sin 120 0 = a 2 3 3
tan B A M = B M A M ⇒ A M = a 3 ⇒ tan S M A = S A A M ⇒ S A = a 3
V S . A B C D = 1 3 . a 3 . a 2 3 3 = a 3 9

Đáp án là B
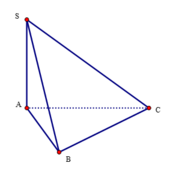
Tam giác SAB vuông tại A có S A 2 = S B 2 - A B 2 = 4 a 2 nên SA= 2a
Có S A B C = 1 2 A B . A C = 2 a 2
Có V = 1 3 S A . S A B C = 4 a 3 3
Đáp án C
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.