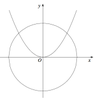
Parabol (P): y = x 2 chia đường tròn (C): x 2 + y 2 = 2 thành hai phần (tham khảo hình vẽ bên) có tỷ số diện tích (phần nhỏ chia phần lớn) bằng
A. 3 π + 2 12 π
B. 3 π + 2 9 π - 2
C. 9 π - 2 12 π
D. 9 π - 2 18 π + 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm:
8
x
-
27
x
3
Giả sử đường thẳng y = m cắt đường cong (C) trong góc phần tư thứ nhất của hệ trục toạ độ tại các điểm có hoành độ 0 < a < b, ta có 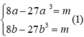 và gọi F(x) là một nguyên hàm của hàm số
f
(
x
)
=
8
x
-
27
x
3
-
m
ta có
và gọi F(x) là một nguyên hàm của hàm số
f
(
x
)
=
8
x
-
27
x
3
-
m
ta có 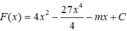 và quan sát hình vẽ có các diện tích hình phẳng kẻ carô và gạch sọc lần lượt là
và quan sát hình vẽ có các diện tích hình phẳng kẻ carô và gạch sọc lần lượt là
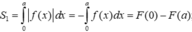
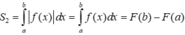
Vì ![]()
![]()
Rút m = 8 x - 27 x 3 từ (1) thay vào (2) có
![]()
![]()
Thay ngược lại (1) có ![]()
Chọn đáp án C.

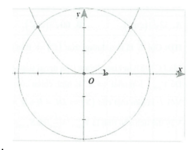

Diện tích phần giới hạn giữa đường tròn và parabol là:
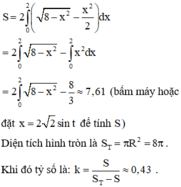
Chọn A.