Cho hình bình hành ABCD ( AB//CD ) có AB = CD = 5cm, độ dài đường cao hình bình hành là h = 4cm. Tính diện tích của hình bình hành?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


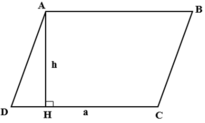
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

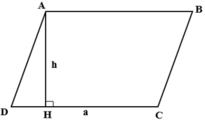
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

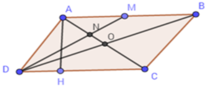
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A

a) Gọi H là chân đường vuông góc kẻ từ A xuống CD
Theo đề bài, ta có: AH=3(cm)
Xét hình bình hành ABCD có AH là đường cao ứng với cạnh CD(gt)
nên \(S_{ABCD}=AH\cdot CD=4\cdot3=12\left(cm^2\right)\)

a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN