Cho điểm P nằm ngoài đường thẳng d. Hãy nêu cách vẽ đường xiên PQ, PR sao cho PQ = PR và ∠(QPR) = 60o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
21 tháng 6 2019
a) Phân tích bài toán
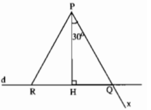
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và\(\widehat{QPR}=60^0\). Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ∆PHQ = ∆PHR (cạnh huyền, cạnh góc vuông), suy ra \(\widehat{HPQ}=\widehat{HPR}=30^0\) Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ\(PH\perp d\) (H ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR. Do HQ = HR nên PQ = PR.
Hơn nữa\(\widehat{QPR}=2\widehat{HQP}=60^0\)
b) Hướng dẫn
- Tam giác PQR có PQ = PR và \(\widehat{QPR}=60^0\), tam giác PQR là tam giác đều
PQ = 18cm => QR =18cm ; HQ = HR =9cm.
21 tháng 6 2019
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60°.
Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ΔPHQ = ΔPHQ (cạnh huyền, cạnh góc vuông),
suy ra ∠(HPQ) = ∠(HPR) = 30°. Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ PH ⊥ d (H ∈ d).
Dùng thước đo góc để vẽ góc HPx bằng 30°.
Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ.
Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR.
Do HQ = HR nên PQ = PR.
Hơn nữa ∠(QPR) = 2∠(HPQ) = 60°.
b) Hướng dẫn
- Tam giác PQR có PQ = PR và ∠(QPR) = 60°, tam giác đó là tam giác đều
- PQ = 18cm ⇒ QR =18 cm ; HQ = HR =9 cm
CM
27 tháng 4 2019
+ Hình chiếu của PQ và PR chính là HQ và HR.
+ ΔPQR có PQ = PR và ∠P = 60o
⇒ ΔPQR đều
⇒ QR = PQ = 18cm.
+ ΔPHQ = ΔPHR ( cạnh huyền- cạnh góc vuông) ⇒ QH = HR = 1/2.QR = 9cm.
Vậy độ dài hình chiếu của PQ và PR trên d đều bằng 9cm.
CM
30 tháng 4 2019
* Vẽ hình:
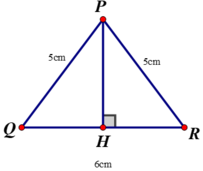
- Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm.
+ Vẽ đoạn thẳng QR = 6cm.
+ Vẽ cung tròn tâm Q và cung tròn tâm R bán kính 5cm. Hai cung tròn này cắt nhau tại P.
+ Nối PQ và PR ta được tam giác cần vẽ.
- Vẽ điểm M : Vẽ cung tròn tâm P bán kính 4,5cm cắt QR (nếu có) tại M.
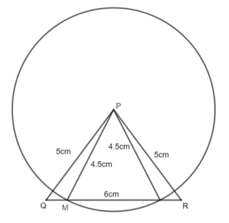
Vậy ta có thể vẽ được 2 điểm M trên đường thẳng QR để PM = 4.5cm
* Kẻ đường cao PH của ΔPQR
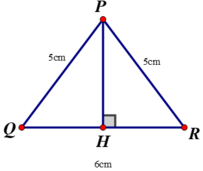
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có
PH chung
PQ = PR ( = 5cm)
⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)
⇒ HQ = HR (Hai cạnh tương ứng)
Mà HQ + HR = QR = 6 cm
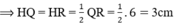
+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)
⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.
Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
⇒ M nằm giữa H và Q hoặc H và R
⇒ M nằm trên cạnh QP và có hai điểm M như vậy.
+ Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60o.
Gọi H là chân đường vuông góc kẻ từ P đến d.
Khi đó ΔPHQ = ΔPHR (cạnh huyền, cạnh góc vuông)
⇒ ∠(HPQ) = ∠(HPR) = 30o.
+ Từ đó suy ra cách vẽ hai đường xiên PQ và PR:
- Kẻ PH ⊥ d (H ∈ d)
- Kẻ các tia Px, Py tạo với PH 1 góc 30o (Py, Px thuộc hai nửa mp bờ là đường thẳng PH)
- Px, Py cắt d lần lượt tại Q và R.
Khi đó ΔPHQ = ΔPHR nên PQ = PR và ∠QPR = 60o.