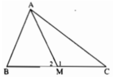
Cho tam giác ABC với AB ≤ AC. Trên cạnh BC lấy một điểm M bất kỳ khác B và C. Chứng minh rằng AM < AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
Sửa đề: AB>=AC
Ta có: \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\left[{}\begin{matrix}\widehat{AMB}>90^0\\\widehat{AMC}>=90^0\end{matrix}\right.\)
Nếu \(\widehat{AMC}>=90^0\) thì ΔAMC có cạnh AC là cạnh lớn nhất
nên AC>AM
Nếu \(\widehat{AMB}>90^0\) thì ΔABM có AB là cạnh lớn nhất
=>AB>AM
mà AB<AC
nên AM<AC
AH
Akai Haruma
Giáo viên
11 tháng 3 2021
Bạn tham khảo lời giải tại đây:
cho tam giác ABC , AB - Hoc24
3 tháng 12 2023
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
=>KM\(\perp\)BC
Xét ΔKBC có
KM là đường cao
KM là đường trung tuyến
Do đó:ΔKBC cân tại K
=>KB=KC
c: ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
\(\widehat{ABF}+\widehat{FBC}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{FBC}=\widehat{ECB}\)
và \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{ACE}\)
=>\(\widehat{EBK}=\widehat{FCK}\)
Xét ΔEBK và ΔFCK có
\(\widehat{EBK}=\widehat{FCK}\)
BK=CK
\(\widehat{EKB}=\widehat{FKC}\)
Do đó: ΔEBK=ΔFCK
ΔABC có AB ≤ AC ⇒ ∠C ≤ ∠B.
ΔABM có ∠M1 là góc ngoài nên ∠M1 > ∠B
⇒ ∠M1 > ∠C
ΔAMC có ∠M1 > ∠C ⇒ AC > AM.