Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu A B → = p A C → t h ì A ' B ' → = p A ' C ' → , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’

+ Chứng minh hoàn toàn tương tự ta được
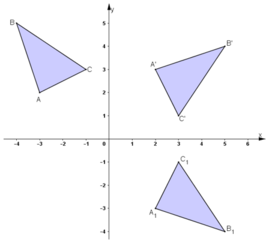
b. ΔA1B1C1 là ảnh của ΔABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90º và phép đối xứng qua trục Ox.
⇒ ΔA1B1C1 là ảnh của ΔA’B’C’ qua phép đối xứng trục Ox.
⇒ A1 = ĐOx(A’) ⇒ A1(2; -3)
B1 = ĐOx(B’) ⇒ B1(5; -4)
C1 = ĐOx(C’) ⇒ C1(3; -1).
a) + Ta có:
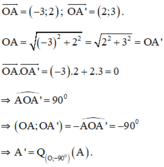

a. Ta có :Vì G đối xứng E qua D nên D là trung điểm EG
Xét tứ giác AGCE có : AC , EG là hai đường chéo
Mà AC cắt EG tại trung điểm mỗi đường
Do đó AGCE là hình bình hành .
Lại có : AE \(\perp\) BC => Góc AEC = 90 độ
Vậy AGCE là hình chữ nhật
b. Ta có : Vì H đối xứng với E qua F nên F là trung điểm HE
Xét tứ giác HAEB có : 2 đường chéo AB , HE
Mà AB cắt HE tại trung điểm mỗi đường
Do đó HAEB là hình bình hành
Lại có : góc AEB = 90 độ
=> HAEB là hình chữ nhật
=> Góc HAE = 90 độ
Mà ta có : AGCE là hình chữ nhật
=> Góc GAE = 90 độ
=> Góc HAE + Góc GAE = 90 độ
Hay góc HAE và góc GAE kề bù
=> H , A , G thẳng hàng



Để ý rằng
Ta có:
Từ đó suy ra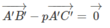
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.