Tìm x biết
a) x + 7 4 = 5
b) 2 x 2 = 9 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

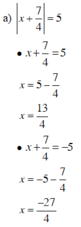


a, \(x=-\dfrac{5}{6}-\dfrac{7}{12}=\dfrac{-10-7}{12}=-\dfrac{17}{12}\)
b, \(\dfrac{2}{9}-x=-\dfrac{4}{3}.\dfrac{5}{6}=-\dfrac{24}{18}=-\dfrac{4}{3}\Leftrightarrow x=\dfrac{2}{9}+\dfrac{4}{3}=\dfrac{14}{9}\)
c, \(-3=x-1\Leftrightarrow x=-2\)
d, \(\dfrac{3}{5}x-\dfrac{2}{3}=\dfrac{4}{5}:\dfrac{1}{5}=4\Leftrightarrow\dfrac{3}{5}x=4+\dfrac{2}{3}=\dfrac{14}{3}\Leftrightarrow x=\dfrac{14}{3}:\dfrac{3}{5}=\dfrac{70}{9}\)

Bài 1:
a) Ta có: \(\dfrac{17}{6}-x\left(x-\dfrac{7}{6}\right)=\dfrac{7}{4}\)
\(\Leftrightarrow\dfrac{17}{6}-x^2+\dfrac{7}{6}x-\dfrac{7}{4}=0\)
\(\Leftrightarrow-x^2+\dfrac{7}{6}x+\dfrac{13}{12}=0\)
\(\Leftrightarrow-12x^2+14x+13=0\)
\(\Delta=14^2-4\cdot\left(-12\right)\cdot13=196+624=820\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{205}}{-24}=\dfrac{-7+\sqrt{205}}{12}\\x_2=\dfrac{14+2\sqrt{2015}}{-24}=\dfrac{-7-\sqrt{205}}{12}\end{matrix}\right.\)
b) Ta có: \(\dfrac{3}{35}-\left(\dfrac{3}{5}-x\right)=\dfrac{2}{7}\)
\(\Leftrightarrow\dfrac{3}{5}-x=\dfrac{3}{35}-\dfrac{10}{35}=\dfrac{-7}{35}=\dfrac{-1}{5}\)
hay \(x=\dfrac{3}{5}-\dfrac{-1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)

Lời giải:
a.
$0< x< \frac{1}{4}+\frac{4}{5}$
$\Rightarrow 0< x< \frac{21}{20}$ hay $0< x< 1,05$
$\Rightarrow x=1$
b.
$\frac{4}{7}+\frac{3}{7}< x< \frac{5}{3}+\frac{2}{3}$
$\Rightarrow 1< x< \frac{7}{3}$
$\Rightarrow x=2$

a) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-3\right)\left(5x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
c) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
d) \(\Rightarrow\left(x-7\right)\left(3x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(a,\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\\ c,\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\\ d,\Leftrightarrow\left(x-7\right)\left(3x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)

b: =>x(8-7)=-33
=>x=-33
c: =>-12x+60+21-7x=5
=>-19x=-76
hay x=4
d: =>-2x-2-x+5+2x=0
=>3-x=0
hay x=3

a) Ta có: \(2\sqrt{9x-27}-\dfrac{1}{5}\sqrt{25x-75}-\dfrac{1}{7}\sqrt{49x-147}=20\)
\(\Leftrightarrow6\sqrt{x-3}-\sqrt{x-3}-\sqrt{x-3}=20\)
\(\Leftrightarrow4\sqrt{x-3}=20\)
\(\Leftrightarrow x-3=25\)
hay x=28
b) Ta có: \(\sqrt{9x+18}-5\sqrt{x+2}+\dfrac{4}{5}\sqrt{25x+50}=6\)
\(\Leftrightarrow3\sqrt{x+2}-5\sqrt{x+2}+4\sqrt{x+2}=6\)
\(\Leftrightarrow2\sqrt{x+2}=6\)
\(\Leftrightarrow x+2=9\)
hay x=7

a: =>2x-x=-5/2-1/3
=>x=-17/6
b: =>4(x-2)2=36
=>(x-2)2=9
=>x-2=3 hoặc x-2=-3
hay x=5 hoặc x=-1
c: =>2x+1/2=5/6
=>2x=1/3
hay x=1/6

a. (x - 22) - 1 = 0
<=> x - 4 - 1 = 0
<=> x = 5
b. 4 - (x - 2)2 = 0
<=> 22 - (x - 2)2 = 0
<=> (2 - x + 2)(2 + x - 2) = 0
<=> x(4 - x) = 0
<=> \(\left[{}\begin{matrix}x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
d. (3x - 2)2 - (2x + 3)2 = 5(x + 4)(x - 4)
<=> (3x - 2 - 2x - 3)(3x - 2 + 2x + 3) = 5(x2 - 16)
<=> (x - 5)(5x + 1) = 5x2 - 80
<=> 5x2 + x - 25x - 5 = 5x2 - 80
<=> 5x2 - 5x2 + x - 25x = -80 + 5
<=> -24x = -75
<=> x = \(\dfrac{25}{8}\)

a: Ta có: \(\left(2x+1\right)^2-4\left(x+2\right)^2=9\)
\(\Leftrightarrow4x^2+4x+1-4x^2-16x-16=9\)
\(\Leftrightarrow-12x=24\)
hay x=-2
b: Ta có: \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\)
\(\Leftrightarrow x^2+6x+9-x^2-4x+32=1\)
\(\Leftrightarrow2x=-40\)
hay x=-20